Submitted to HEJ
Manuscript no.: ANM-010201-A
|  

 |
|
We have seen that some functions cannot be integrated in terms of
elementary functions. This is not as bad as you may expect, because in
practice it often suffices to find an approximate value of the
definite integral and there exists good methods of numerical
approximation.
We shall now discuss the simplest and most obvious methods called
quadrature techniques. We wish to direct special attention to
the fundamental fact that the meaning of an approximate calculation is
not precise unless it is supplemented by an estimate of the errors
occurring.
The notations and conventions used here are:
where 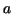 and and 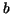 are constants are constants 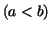 and and 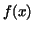 is given as a continuous
differentiable function. Then we know that the integral exists.
We have seen in Chapter 2 that we may restrict to regular subdivisions,
therefore let the interval of integration be divided into is given as a continuous
differentiable function. Then we know that the integral exists.
We have seen in Chapter 2 that we may restrict to regular subdivisions,
therefore let the interval of integration be divided into 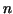 equal parts of
length equal parts of
length  . We denote the points of subdivisions by . We denote the points of subdivisions by
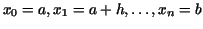 , and the values of the function at the points of division by , and the values of the function at the points of division by
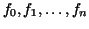 .
Similarly, the values of the function at the midpoints of the
intervals by .
Similarly, the values of the function at the midpoints of the
intervals by
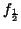 , ,
 . It is fairly natural to use the Riemann sum approximation to . It is fairly natural to use the Riemann sum approximation to 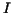 , as
we did it in section 2. The procedure subdiv(a,b,n) -- we shall use it in the next examples -- returns a regular subdivision , as
we did it in section 2. The procedure subdiv(a,b,n) -- we shall use it in the next examples -- returns a regular subdivision
![$[a=x_{0},x_{1},\ldots,x_{n}=b]$](img407.gif) . .
EXAMPLE 6.1.
 f:=x->1/x: S:= subdiv(1,2,10):
 integral_plot(f,S,'riemann');
 upper(f,S);
 lower(f,S);
We have a lower approximation for 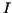 as as 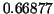 and an upper one, which is and an upper one, which is 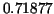 . These differ by . These differ by 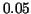 so there may be an error greater then 7% if either of
these values is taken as an estimate for the integral. ``OK, let us
simply choose a finer subdivision and we shall get a better
approximation'' would be the next idea. Observe, however, that we have
to calculate the minimum (or the maximum) of the function in every
subinterval so there may be an error greater then 7% if either of
these values is taken as an estimate for the integral. ``OK, let us
simply choose a finer subdivision and we shall get a better
approximation'' would be the next idea. Observe, however, that we have
to calculate the minimum (or the maximum) of the function in every
subinterval
![$[x_{i},x_{i + 1}]$](img419.gif) ,
which is rather costly and error-prone. This method is easy
to apply if the integrand ,
which is rather costly and error-prone. This method is easy
to apply if the integrand  is known to be monotonic. And the other
cases? The technique mentioned above is not a very good one from practical
point of view. We require better techniques to satisfy two important
criteria: is known to be monotonic. And the other
cases? The technique mentioned above is not a very good one from practical
point of view. We require better techniques to satisfy two important
criteria:
- The technique should give results of high accuracy.
- The technique should require only a small number of function
evaluations.
In most cases the Riemann-sum method does not satisfy the criteria 1
and 2 but it enables us to formulate other methods realizing better
these desirable properties. The most obvious method for approximating
to 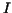 without calculating maximum (or minimum) values on the subintervals is
directly connected with the good old stepfunctions. For the value of
the stepfunction on without calculating maximum (or minimum) values on the subintervals is
directly connected with the good old stepfunctions. For the value of
the stepfunction on
![$[x_{i},x_{i + 1}]$](img422.gif) we choose we choose  .
Then for the integral we have got an approximate expression: .
Then for the integral we have got an approximate expression:
This method is called rectangle rule. (Here and hereafter
the symbol 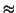 means ``is approximately equal to''.) means ``is approximately equal to''.)
EXAMPLE 6.2.
 f:=x->x^(1/2)*sin(x)*cos(x): n:=6: S:=subdiv(0,2,n):
 integral_plot(f,S,'rectangle');
 int_num(f,S,'rectangle');
We obtain a closer approximation with no greater trouble if we replace
the rectangle area by a trapezoid area
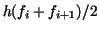 .
For the whole integral this gives the approximate expression: .
For the whole integral this gives the approximate expression:
This is the trapezoid formula, since, when the areas of
the trapezoids are added, each value of the function except the first
and the last occurs twice.
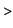 integral_plot(f,S,'trapezoid');
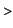 int_num(f,S,'trapezoid');
The approximation becomes even better if instead of choosing
the trapezoid under a chord we chose the trapezoid under the tangent
to the curve at the point with the abscissa
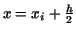 .
The area of this trapezoid is simply .
The area of this trapezoid is simply
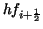 , and the
approximation for the entire integral is , and the
approximation for the entire integral is
which is called the tangent formula. Let us see how it is work.
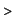 integral_plot(f,S,'tangent');
 int_num(f,S,'tangent');
The next method is called mid-point rule. In this case we
assume the function values between 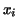 and and 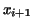 are constant and
have the value equal to the function value at are constant and
have the value equal to the function value at
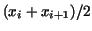 . .
 integral_plot(f,S,'mid-point');
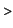 int_num(f,S,'mid-point');
Observe, that the values of the approximating integral in the case of
the tangent method and the mid-point method are the same. Is it a
coincidence? Explain why not.
The next method depends on estimating the subarea of the integral at
two adjacent subintervals, i.e. between the abscissa
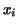 and and
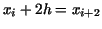 by considering the upper boundary to be no longer a straight line
but a parabola. To be more precise, the parabola which passes through
the three points of the curve with abscissa
by considering the upper boundary to be no longer a straight line
but a parabola. To be more precise, the parabola which passes through
the three points of the curve with abscissa 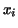 , , 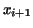 , , 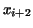 . The equation of the parabola is . The equation of the parabola is
Exercise 6.1. Prove the latter statement.
After a brief calculation we get the area under the parabola:
If we assume that 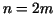 , i.e. that , i.e. that  is even, by the addition of the
subareas we obtain the Simpson's rule: is even, by the addition of the
subareas we obtain the Simpson's rule:
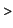 integral_plot(f,S,'simpson');
 int_num(f,S,'simpson');
The integral of 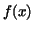 can also be expressed in closed form. can also be expressed in closed form.
 Int(x^(1/2)*sin(x)*cos(x),'x'=0..2)=int(f(x),'x'=0..2);
(If you don't agree, feel free to check!) The approximate value:
 evalf(int(x^(1/2)*sin(x)*cos(x),'x'=0..2));
It is worth to compare the results getting by the different methods:
- Rectangle rule: .3903146893
- Trapezoid rule: .3011246599
- Tangent rule: .3187318652
- Simpson's rule: .3141154642
- Maple approximation of the closed form: .3126735508
In our example the Simpson's rule seems to be the best concerning the
criteria 1 and 2. Is this always true or only a coincidence again? We need an estimation of the
error.
Estimations can be easily given for each of our methods, if bounds for
the derivatives of the function 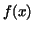 are known throughout the interval
of integration. Let are known throughout the interval
of integration. Let
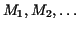 be upper bounds for the absolute
values of the first, second, be upper bounds for the absolute
values of the first, second, 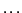 derivatives, i.e. we assume that throughout the interval
derivatives, i.e. we assume that throughout the interval
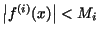 for all for all 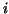 .
Then the estimation formulas are as follows: .
Then the estimation formulas are as follows:
- Rectangle rule:
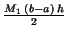 , ,
- Tangent rule:
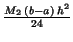 , ,
- Trapezoid rule:
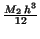 , ,
- Simpson's rule:
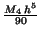 . .
From the last two estimates there also follow estimates for the entire
integral. We see, that Simpson's rule has an error of much higher
order in the small quantity  than the others, so that where than the others, so that where 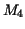 is not too large, it is very advantageous for practical
calculations. The proofs of the estimates are quite simple using the
Taylor's theorem and can be found in every textbooks on numerical
methods.
is not too large, it is very advantageous for practical
calculations. The proofs of the estimates are quite simple using the
Taylor's theorem and can be found in every textbooks on numerical
methods.
There are other kinds of very important quadrature methods based on
orthogonal polynomials (Gaussian quadratures). There are known (and
used) methods if the integrand  is not finite or
one of its derivatives is infinite at some point in is not finite or
one of its derivatives is infinite at some point in ![$[a,b]$](img482.gif) (singular
integrals). In many cases miscellaneous techniques are also
available (series expansions, Laplace or Fourier transforms). (singular
integrals). In many cases miscellaneous techniques are also
available (series expansions, Laplace or Fourier transforms).
Exercise 6.2.
(a) Take a larger value for 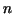 , the number of subintervals, redo the
numerical integrations above and check the improvements in the
approximations. , the number of subintervals, redo the
numerical integrations above and check the improvements in the
approximations.
(b) The numerical computations can be improved by allow a higher
value to the built-in Maple variable Digits. E.g.
 Digits:=20: int_num(f,S,'simpson'); Digits:=10:
Recompute the numerical integral values of EXAMPLE 5.2
using 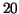 decimal ``Digits''. decimal ``Digits''.
(c) Calculate
 Int(exp(-x^2),'x'=0..infinity);
to within  . .
(d) From the formula
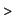 Pi/4 = Int(1/(1+x^2),'x'=0..1);
calculate 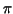
- using the trapezoid formula with
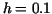 , ,
- using Simpson's rule with
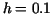 . .
(e) Calculate
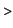 Int(1/(sqrt(1+x^4)),'x'=0..1);
numerically with an error less than 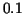 . .
Exercise 6.3.
Using the trapezoid rule with 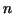 subdivisions -- let us denode the integral approximation by subdivisions -- let us denode the integral approximation by 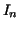 -- calculate the following integrals with -- calculate the following integrals with
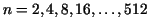 . .
Exercise 6.4.
Repeat the previous exercise using Simpson's rule.
| Submitted to HEJ
Manuscript no.: ANM-010201-A
|  

 |
|
![\includegraphics[width=12cm]{int07.ps}](img410.gif)
![\includegraphics[width=12cm]{int08.ps}](img428.gif)
![\includegraphics[width=12cm]{int09.ps}](img434.gif)
![\includegraphics[width=12cm]{int10.ps}](img441.gif)
![\includegraphics[width=12cm]{int11.ps}](img448.gif)
![\includegraphics[width=12cm]{int12.ps}](img462.gif)