HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-981030-A
| 

 |
|
- 1
-
D. N. Arnold, R. S. Falk, and R. Winther.
Preconditioning in 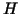 (div) and applications. (div) and applications.
Mathematics of Computation, 66, 1997.
To appear. Preprint available via
http://www.math.psu.edu/dna/papers/hdiv.ps or hdiv.dvi.
- 2
-
O. Bíró.
Numerische Aspekte von Potentialformulierungen in der
Elektrodynamik.
Habilitationsschrift, Technische Universität Graz, 1992.
- 3
-
D. Braess.
Finite Elemente - Theorie, schnelle Löser und Anwendungen
in der Elastizitätstheorie.
Springer-Lehrbuch. Springer Verlag, Berlin, Heidelberg, 1992.
- 4
-
F. Brezzi and M. Fortin.
Mixed and Hybrid Finite Element Methods.
Number 15 in Springer Series in Computational Mathematics.
Springer-Verlag, Berlin, 1991.
- 5
-
M. Costabel and M. Dauge.
Singularities of Maxwell's equations on polyhedral domains.
Prépublication 96-30, Institut de Recherche Mathématique de
Rennes, December 1996.
- 6
-
V. Girault and P.-A. Raviart.
Finite Element Approximation of the Navier-Stokes Equations.
Number 749 in Lecture Notes in Mathematics. Springer-Verlag, Berlin,
1979.
- 7
-
V. Girault and P.-A. Raviart.
Finite Element Methods for Navier-Stokes Equations.
Number 5 in Springer Series in Computational Mathematics.
Springer-Verlag, Berlin, 1986.
- 8
-
B. Heise.
Analysis of a fully discrete finite element method for a nonlinear
magnetic field problem.
SIAM J. Numer. Anal., 31(3):745-759, 1994.
- 9
-
B. Heise.
A mixed variational formulation for 3D magnetostatics and its
finite element discretization.
Technical Report 96-6, Universität Linz, Institut für Mathematik,
Arbeitsgruppe Numerische Mathematik und Optimierung, 1996.
- 10
-
B. Heise and M. Kuhn.
Parallel solvers for linear and nonlinear exterior magnetic field
problems based upon coupled FE/BE formulations.
Computing, 56(3):237-258, 1996.
- 11
-
A. Kameari and K. Koganezawa.
Convergence of ICCG method in FEM using edge elements without
gauge condition.
1996.
Proc. of the IEEE CEFC Conference, Okayama, Japan, March 18 - 20,
1996.
- 12
-
R. C. Mesquita.
Additional properties of the incomplete gauge formulation for 3-D
finite-element magnetostatics.
IEEE Transactions on Magnetics, MAG-30:2861-2864, 1994.
- 13
-
I. Nishiguchi, H. Matsuzawa, and M. Sasaki.
A comparative study of magnetostatics using three-field formulation
and conventional vector potential formulations.
1996.
Proc. of the IEEE CEFC Conference, Okayama, Japan, March 18 - 20,
1996.
- 14
-
K. Preis, I. Bardi, O. Biro, C. Magele, G. Vrisk, and K. R. Richter.
Different finite element formulations of 3D magnetostatic fields.
IEEE Transactions on Magnetics, MAG-28:1056-1059, 1992.
- 15
-
D. Rodger.
Finite-element method for calculating power frequency 3-dimensional
electromagnetic field distributions.
IEE Proceedings - A, 130:233-238, 1983.
- 16
-
D. Rodger and P. J. Leonard.
Modelling the electromagnetic performance of moving rail gun
launchers using finite elements.
IEEE Transactions on Magnetics, 29:496-498, 1993.
- 17
-
Y. G. Soloveitchik.
Mathematical model of three-dimensional electro-magnetic fields in
electrotechnical devices.
Preprint UDK 621.37, Novosibirsk Electrotechnical Institute, 1990.
In Russian.
- 18
-
S. Williamson and E. K. C. Chan.
Three-dimensional finite-element formulation for problems involving
time-varying fields, relative motion, and magnetic saturation.
IEE Proceedings - A, 140:121-130, 1993.
- 19
-
E. Zeidler.
Vorlesungen über nichtlineare Funktionalanalysis II:
Monotone Operatoren, volume 9 of Teubner-Texte zur Mathematik.
Teubner-Verlag, Leipzig, 1977.
| HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-981030-A
| 

 |
|