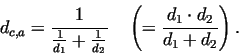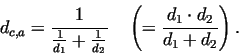HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-991102-A
| 

 |
|
We initiate distances in the following manner (our graphs are directed):
- a)
- edge
Let us denote the distance from condition
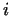 to condition to condition 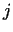 with with
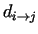 . In the simplest case all of the distances are . In the simplest case all of the distances are 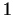 , but
usually , but
usually
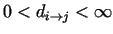 . .
- b)
- way
Going on subsequent edges the distances are summarized, so the
distance is additive.
- c)
- between two nodes
In this case we have to consider all of the ways connecting these two nodes.
Thus, according to real life
for the resultant distance
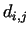 we have we have
 min min
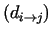 . The equality can holds only in
degenerated cases, if one of the . The equality can holds only in
degenerated cases, if one of the
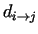 -s is -s is 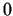 or if all of the or if all of the
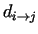 -s are -s are 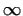 .
Of course, usually .
Of course, usually
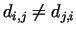 . .
- d)
- between a node and a set (of nodes)
Similarly, as in point c).
EXAMPLE
Let us assume, that in a whole-type distance model from condition 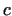 we can reach 2 dangerous conditions,
we can reach 2 dangerous conditions, 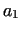 and and 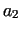 with distances with distances
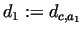 and and
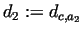 , respectively. , respectively.
System:
 a a
 c c
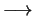 a a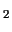
In this case obviously 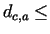 min min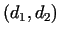 , where , where  symbolizes
the resultant danger condition, and symbolizes
the resultant danger condition, and 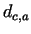 depends on depends on 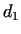 and and
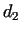 . If e.g. . If e.g. 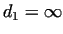 , then , then  . A possible solution for
this problem is the use of the harmonic average, so we get . A possible solution for
this problem is the use of the harmonic average, so we get
| HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-991102-A
| 

 |
|