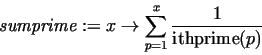HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-000926-A |  
![[*]](http://heja.szif.hu/Icons/vissza1.gif)
![[*]](http://heja.szif.hu/Icons/elore1.gif) |
|
Results in the ancient time
THEOREM 3.
The number of primes is infinite.
PROOF. (By EUCLID)
Let us assume, that there are only finite prime numbers,
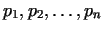 . Let us consider the number . Let us consider the number
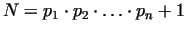 . This number is not divisible
by the primes listed above, and the number . This number is not divisible
by the primes listed above, and the number  is not listed as a prime number,
so it cannot be written in the form of Theorem 2. But this is not possible,
thus is not listed as a prime number,
so it cannot be written in the form of Theorem 2. But this is not possible,
thus 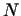 is a new prime itself, or the product of new primes not listed. is a new prime itself, or the product of new primes not listed.
> ifactor(2*3*5*7*11*13*17+1);
PROPOSITION 1.
If a number  has a prime divisor has a prime divisor 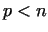 , then it has a prime
divisor , then it has a prime
divisor
![$p_1 \le [\sqrt{n}]$](img28.gif) . .
Using this result, we are able to specify the prime numbers until 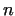 , if we
know the primes until , if we
know the primes until ![$[\sqrt{n}]$](img30.gif) . The following method is called
the sieve of ERATOSTHENES after the author.
Let us write the positive integer numbers beginning with 2 (or 1). Let us
consider the first number in the list (we erase and skip the number 1), and
erase its multiples. After it we take the
following non-erased number in the list, and repeat the procedure. If we
reach a non-erased number greater than . The following method is called
the sieve of ERATOSTHENES after the author.
Let us write the positive integer numbers beginning with 2 (or 1). Let us
consider the first number in the list (we erase and skip the number 1), and
erase its multiples. After it we take the
following non-erased number in the list, and repeat the procedure. If we
reach a non-erased number greater than 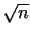 , then the sieving is
complete. , then the sieving is
complete.
After these results there was only very limited development in the prime
number theory until the 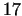 th century, FERMAT's time. In the
following the most important results of the past four centuries will be
summarized. th century, FERMAT's time. In the
following the most important results of the past four centuries will be
summarized.
The number of primes
Let us denote the number of prime elements less-equal to  by by 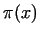 ,
where ,
where 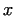 is a positive real number.
From the result of EUCLID follows, that is a positive real number.
From the result of EUCLID follows, that
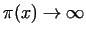 ,
if ,
if
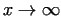 . Already EULER noted, that . Already EULER noted, that
 . This was first proved by
LEGENDRE.
The following very important theorem was conjectured in the late 1790s
by LEGENDRE and GAUSS, and first
proved by HADAMARD and DE LA VALLÉE POUSSIN (1896) with
extremely complicated mathematical tools. Elementary proof was given first
by PAUL ERDOS and A. SEELBERG (1948). . This was first proved by
LEGENDRE.
The following very important theorem was conjectured in the late 1790s
by LEGENDRE and GAUSS, and first
proved by HADAMARD and DE LA VALLÉE POUSSIN (1896) with
extremely complicated mathematical tools. Elementary proof was given first
by PAUL ERDOS and A. SEELBERG (1948).
THEOREM 4.
The big prime number theorem
REMARKS
1. The notation 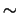 means "asymptotic equal" i.e. means "asymptotic equal" i.e.
2. Let us denote the 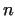 th prime number by th prime number by  .
From the result of the theorem follows .
From the result of the theorem follows
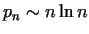 .
3. The approach presented in Theorem 4. can be improved with .
3. The approach presented in Theorem 4. can be improved with
To illustrate the results of the theorem with Maple, we write the function
 , and delineate it with , and delineate it with
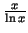 in a logarithmic coordinate-system. in a logarithmic coordinate-system.
> a[2]:=0:
> for i from 3 to 10000 do a[i]:=a[i-1]:
> if isprime(i-1) then a[i]:=a[i]+1 fi:
> od:
> pi:=x->if x=trunc(x) then a[x] else a[trunc(x+1)] fi:
> with(plots):
> loglogplot(\{x/ln(x),pi(x)\},x=1.2..500,y=1..200);
By studying the figure we can see the stepfunction-like behaviour of 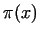 (plotted above), and the fact, that for larger numbers both of the functions
fit tight the same asymptotic line. However, between two asymptotic equal
functions it is allowed to be very large differences.
(plotted above), and the fact, that for larger numbers both of the functions
fit tight the same asymptotic line. However, between two asymptotic equal
functions it is allowed to be very large differences.
> pi(10000); evalf(10000/ln(10000));
> ""/";
To point 2. of the Theorem, we can produce the 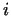 th prime number with
the function th prime number with
the function ithprime.
> ithprime(1000), evalf(1000*ln(1000));
THEOREM 5. (First proved by EULER)
The sum of the reciprocal value of prime numbers is infinite, i.e.
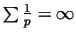 . .
REMARKS
1. Comparing with the sum of the reciprocal value of square
numbers we get
so the prime numbers are situated more densely.
2. It is true moreover, that
Similarly as above, we write the functions
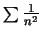 and and
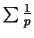 to test their behaviour. to test their behaviour.
> sumsquare:=x->sum(1/n^2,n=1..x);
> sumprime:=x->sum(1/ithprime(p),p=1..x);
> evalf(sumsquare(1000)), evalf(sumprime(1000));
The function 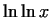 grows very slowly. grows very slowly.
> evalf(ln(ln(1000))),evalf(ln(ln(1000000)));
The distance of primes
Analysing the result of Theorem 4., we conclude that the primes gradually
become rarer and rarer (on the average). Their distribution is nevertheless irregular.
For example it is obvious, that the sequence
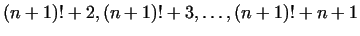 contains no primes, at the same time we know very large consecutive primes.
Let us denote the difference of the
contains no primes, at the same time we know very large consecutive primes.
Let us denote the difference of the  th and th and  th prime number by th prime number by
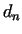 , i.e. , i.e.
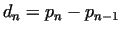 . There are very important results for large
and small prime differences.
From Theorem 4. follows that given an arbitrary small number . There are very important results for large
and small prime differences.
From Theorem 4. follows that given an arbitrary small number 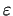 there are infinitely many numbers
there are infinitely many numbers 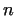 for which
a) for which
a)
 ,
b) ,
b)
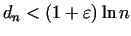 .
One of the important results for large prime differences was stated by
BERTRAND and proved by
CSEBISEV, namely if .
One of the important results for large prime differences was stated by
BERTRAND and proved by
CSEBISEV, namely if 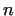 is a positive integer, then there is always
(at least one) prime number between is a positive integer, then there is always
(at least one) prime number between 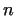 and and 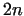 .
We know moreover, that there exists a constant number .
We know moreover, that there exists a constant number 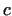 , that
for every suitable large number , that
for every suitable large number 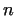 satisfies
satisfies 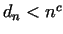 , e.g. , e.g.  can be written.
It is an open question, however, that between two consecutive square numbers
falls in every case a prime number.
If can be written.
It is an open question, however, that between two consecutive square numbers
falls in every case a prime number.
If 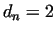 , than we call the numbers , than we call the numbers 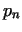 and and 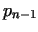 twin primes.
It is a very old conjecture, that there are infinitely many twin primes.
Let us denote the number of twin primes less equal than twin primes.
It is a very old conjecture, that there are infinitely many twin primes.
Let us denote the number of twin primes less equal than 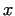 by by 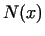 .
The most important result here is, that there exists a positive constant .
The most important result here is, that there exists a positive constant 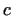 ,
for which ,
for which
 .
Considering the prime number theorem this means that .
Considering the prime number theorem this means that 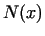 is small compared with
is small compared with 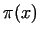 .
To collect observations with Maple about the prime distances we can write
programs with the tools reviewed above. Here a simple example will be
presented, searching twin primes in a given interval. .
To collect observations with Maple about the prime distances we can write
programs with the tools reviewed above. Here a simple example will be
presented, searching twin primes in a given interval.
> twinprimes:=proc(a,limit)
> local i,prev,act;
> prev:=isprime(a);
> for i from a by 2 to a+limit do
> act:=isprime(i);
> if prev and act then lprint(i-2,i) fi; prev:=act
> od
> end:
> twinprimes(10^9+1, 1000);
1000000007 1000000009
1000000409 1000000411
1000000931 1000000933
To find the prime neighbours of an arbitrary number we can use the functions
prevprime and nextprime, too.
> b:=12345678901234567890:
> prevprime(b), nextprime(b);
| HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-000926-A |  
![[*]](http://heja.szif.hu/Icons/vissza1.gif)
![[*]](http://heja.szif.hu/Icons/elore1.gif) |
|
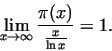
![\includegraphics [width=9cm, angle=270]{p03a01.eps}](img48.gif)