HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-000926-A |  
![[*]](http://heja.szif.hu/Icons/vissza1.gif)
![[*]](http://heja.szif.hu/Icons/elore1.gif) |
|
The great mathematicians for centuries were trying to give formulas, which
would always produce primes, or at least infinitely many primes.
For the second part
of this question a nice answer was given by the following theorem, which
analyses the occurence of prime numbers in arithmetic sequences.
THEOREM 6. (BY DIRICHLET)
Let 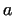 and and 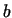 be integer numbers, for which gcd be integer numbers, for which gcd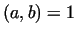 . In this case
the sequence . In this case
the sequence 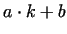 produces infinitely many primes produces infinitely many primes 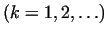 . .
REMARKS
1. As special cases of Theorem 6., there are infinitely many primes
in the form
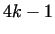 , , 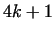 , , 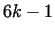 , , 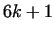 .
2. We can rephrase the results as follows: the polynomial .
2. We can rephrase the results as follows: the polynomial 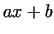 with gcd
with gcd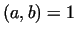 produces infinitely many primes. In this context we can
formulate some other questions, e.g.
a) Is there a polynomial in the form produces infinitely many primes. In this context we can
formulate some other questions, e.g.
a) Is there a polynomial in the form 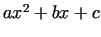 , which produces
infinitely many primes?
b) Is there a polynomial which always produces prime numbers?
In the first case it is easy to prove, that necessary
conditions are the irreducibility of the polynomial and
gcd , which produces
infinitely many primes?
b) Is there a polynomial which always produces prime numbers?
In the first case it is easy to prove, that necessary
conditions are the irreducibility of the polynomial and
gcd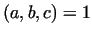 , but
the complete answer is still unknown. To question b), for , but
the complete answer is still unknown. To question b), for
if 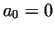 then then 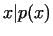 ,
if ,
if 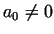 then then 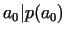 , so the answer is no.
This answer was already given by LEGENDRE.
There are some polynomials, which seem to be good for a lot of substitution
values. EULER has presented the example , so the answer is no.
This answer was already given by LEGENDRE.
There are some polynomials, which seem to be good for a lot of substitution
values. EULER has presented the example 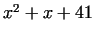 , which
produces prime numbers for , which
produces prime numbers for
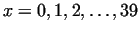 , however for , however for 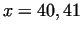 and
other larger values we get composite numbers. and
other larger values we get composite numbers.
> p:=x->x^2+x+41:
> for i from 0 to 45 do
> if not isprime(p(i)) then lprint(i,p(i)) fi:
> od;
40 1681
41 1763
44 2021
In spite of the answer given for part b), theoretically is it possible to give
a formula which
always produces prime numbers. In 1947 H. MILLS proved, that there
exists a real number 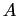 , for which , for which ![$[A^{3^n}]$](img113.gif) is always prime for an
arbitrary positive integer is always prime for an
arbitrary positive integer 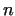 . However, we do not know the value of
this number. . However, we do not know the value of
this number.
Fermat numbers
On the way to find a prime formula, in the 1640s
FERMAT drafted, that the numbers 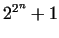 are always prime.
He established, that
beside the small numbers are always prime.
He established, that
beside the small numbers
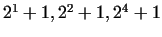 and and 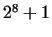 still still 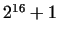 is a prime, too. With the
number
is a prime, too. With the
number 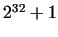 he and his contemporaries could not reach any result, only in
roughly 100 years it was proved by EULER that 641 is a divisor of he and his contemporaries could not reach any result, only in
roughly 100 years it was proved by EULER that 641 is a divisor of
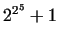 (with establishing first, that a divisor must be in the form (with establishing first, that a divisor must be in the form
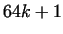 ). Nowadays we know moreover, that the Fermat numbers for ). Nowadays we know moreover, that the Fermat numbers for
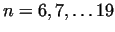 and for more other and for more other 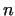 values are not primes. We do not know
however, if there are another Fermat primes or not.
To produce the Fermat numbers in Maple we use the functions values are not primes. We do not know
however, if there are another Fermat primes or not.
To produce the Fermat numbers in Maple we use the functions
fermat or F from the package numtheory.
> with(numtheory):
Warning, new definition for order
> 2^(2^`5`)=F(5), ifactor(fermat(5));
> F(8);
> isprime(fermat(8));
REMARKS
1.
If 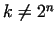 , then , then 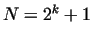 can not be prime. In this case the exponent
can be written in the form can not be prime. In this case the exponent
can be written in the form 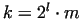 , where , where 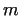 is an odd number.
Thus is an odd number.
Thus
i.e.
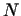 is divisible by is divisible by 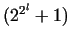 .
2.
The Fermat primes play a very important role in geometry in relation
with the construction of regular poligons (GAUSS, see e.g. in
[9]). .
2.
The Fermat primes play a very important role in geometry in relation
with the construction of regular poligons (GAUSS, see e.g. in
[9]).
Mersenne numbers
After a few years of FERMAT's notice, MERSENNE
published his examination relating to the numbers in the form 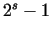 .
He declared, that these numbers are primes if and only if the exponent is .
He declared, that these numbers are primes if and only if the exponent is
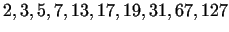 or or 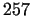 - assuming that the exponent
is less equal than - assuming that the exponent
is less equal than 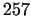 (it was known already in that time, that if (it was known already in that time, that if
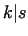 , then , then
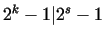 , thus , thus 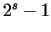 can be only prime, if can be only prime, if 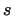 is
prime).
His assertion was not entirely correct, but the
first mistake was found only after more than 200 years. É. LUCAS
proved in the 1870s that is
prime).
His assertion was not entirely correct, but the
first mistake was found only after more than 200 years. É. LUCAS
proved in the 1870s that 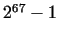 is not prime. After this some other
mistakes were found in the list.
The numbers in the form above are called
Mersenne numbers, and if they are primes, then their names are Mersenne primes.
Nowadays we know more than 30 Mersenne primes.
To produce the Mersenne numbers in Maple we use the functions is not prime. After this some other
mistakes were found in the list.
The numbers in the form above are called
Mersenne numbers, and if they are primes, then their names are Mersenne primes.
Nowadays we know more than 30 Mersenne primes.
To produce the Mersenne numbers in Maple we use the functions
M
or mersenne
from the package numtheory. The result
is the false value if the current Mersenne number is not prime.
Using the functions with double parentheses ![$([i])$](img144.gif) we get exactly the we get exactly the
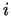 th Mersenne prime. th Mersenne prime.
> mersenne([9]);
> 2^9-1, M(9);
> M(127);
With these tools we are immediately able to find some mistakes in
MERSENNE's list.
> 2^67-1, mersenne(67);
> M(89);
REMARK
In the modern history of mathematics the largest known primes were always
Mersenne primes. For example from 1772 through a century the number 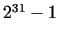 (proved by EULER), until 1950 the number
(proved by EULER), until 1950 the number 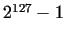 (proved by
É. LUCAS and E. FAUQUEMBERGUE). After this time more
Mersenne primes were
found with computers, in the past few years since 1985 the largest was (proved by
É. LUCAS and E. FAUQUEMBERGUE). After this time more
Mersenne primes were
found with computers, in the past few years since 1985 the largest was
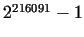 . From 12.01.1994 the largest is . From 12.01.1994 the largest is 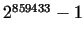 . .
Perfect numbers
We call a number perfect, if the sum of its divisors - not considering the
number itself
- is the same as the number (or using the number theoretical function
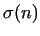 - the sum of divisors - - the sum of divisors -
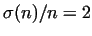 ).
For example for 6, ).
For example for 6, 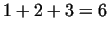 .
Such numbers were already investigated by the ancient Greeks, the notion was
first mentioned by PLATON. Until the Middle Ages mysterious
properties were atributed to perfect numbers.
It is not hard to prove, that an even number is perfect if and only if it is
in the form of .
Such numbers were already investigated by the ancient Greeks, the notion was
first mentioned by PLATON. Until the Middle Ages mysterious
properties were atributed to perfect numbers.
It is not hard to prove, that an even number is perfect if and only if it is
in the form of
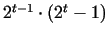 , where , where
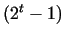 is a Mersenne prime. Thus the investigation of perfect numbers is
closely related with Mersenne primes. The first 4 perfect numbers were
already known by the ancient mathematicians, additional 3 were discovered in
the 15-16th century, till MERSENNE's time.
We know, that the last digit of an even perfect number must be 6 or 8.
Until now nobody could find any odd perfect number, and it seems, that in the
near future we have no hope to prove, that an odd perfect number could not
exist. In any case, if such number exists, it must be very large...
To the examination of the perfect numbers with Maple we can use the function is a Mersenne prime. Thus the investigation of perfect numbers is
closely related with Mersenne primes. The first 4 perfect numbers were
already known by the ancient mathematicians, additional 3 were discovered in
the 15-16th century, till MERSENNE's time.
We know, that the last digit of an even perfect number must be 6 or 8.
Until now nobody could find any odd perfect number, and it seems, that in the
near future we have no hope to prove, that an odd perfect number could not
exist. In any case, if such number exists, it must be very large...
To the examination of the perfect numbers with Maple we can use the function
sigma. Fast "control" can be done with the function divisors.
> c:=2^12*(2^13-1), sigma(c)-c;
> divisors(8192);
We call a number 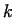 -times perfect, if -times perfect, if
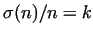 for for
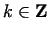 . These
numbers were already investigated by MERSENNE, DESCARTES and
FERMAT. Nowadays we know already 334 . These
numbers were already investigated by MERSENNE, DESCARTES and
FERMAT. Nowadays we know already 334 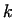 -times perfect numbers, until
the value of -times perfect numbers, until
the value of 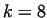 ([4]). ([4]).
> d:=1476304896, sigma(d)/d;
With the generalization of this notion
we can investigate "perfect-like" numbers, where there is a relation
between the sum of divisors not considering the number itself
(
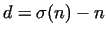 ) and the number ) and the number 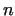 , such as , such as
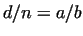 or or 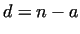 ,
where ,
where 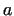 and and 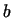 are (positive) integers. are (positive) integers.
> e:=3^2*(3^3-1), (sigma(e)-e)/e;
We have used a Maple program to produce the following results:
| Relation |
Numbers |
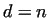 |
6, 28, 496, 8128 |
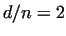 |
120, 672 |
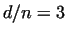 |
30240, 32760 |
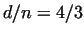 |
12, 234 |
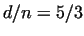 |
84, 270, 1488, 1638, 24384 |
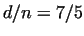 |
30, 140, 2480, 6200, 40640 |
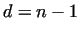 |
1, 2, 4, 8, 16, ... |
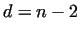 |
3, 10, 136 |
Some results in this tabular are obvious, e.g. in the line 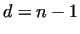 there are pure 2 powers, since
there are pure 2 powers, since
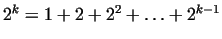 . .
| HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-000926-A |  
![[*]](http://heja.szif.hu/Icons/vissza1.gif)
![[*]](http://heja.szif.hu/Icons/elore1.gif) |
|