HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-000926-A |  
![[*]](http://heja.szif.hu/Icons/vissza1.gif)
![[*]](http://heja.szif.hu/Icons/elore1.gif) |
|
In this subsection we discuss, how we can find the prime factors of a large
number 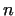 (knowing that (knowing that 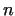 is not prime). If is not prime). If 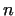 contains e.g. more
than contains e.g. more
than 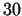 digits the use of the basic algorithm is usually
hopeless, we do not like
a lot of time to wait. In the last decades more algorithms were established
to improve this situation. However, in comparison with the prime tests, the
factorization algorithms are much more expensive.
It is much more difficult to factorize a number,
than to decide the prime property. digits the use of the basic algorithm is usually
hopeless, we do not like
a lot of time to wait. In the last decades more algorithms were established
to improve this situation. However, in comparison with the prime tests, the
factorization algorithms are much more expensive.
It is much more difficult to factorize a number,
than to decide the prime property.
The Pollard-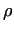 method
One of the well-known methods was presented by J. M. POLLARD.
It was called by him a Monte Carlo method, because of its (pseudo) random
nature. In spite of this the algorithm terminates usually succesful, and it
is easy to programize.
Let method
One of the well-known methods was presented by J. M. POLLARD.
It was called by him a Monte Carlo method, because of its (pseudo) random
nature. In spite of this the algorithm terminates usually succesful, and it
is easy to programize.
Let 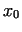 be an integer, and let be an integer, and let 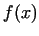 be a polynomial with integer
coefficients. Let us consider the sequence be a polynomial with integer
coefficients. Let us consider the sequence
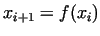 mod mod 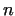 . Our
purpose is, that this sequence must necessarily be random-like. This property
depends on
the choice of the polynomial . Our
purpose is, that this sequence must necessarily be random-like. This property
depends on
the choice of the polynomial 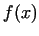 . It is proved, that a linear polynomial . It is proved, that a linear polynomial
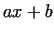 is not good, the next simplest case is is not good, the next simplest case is 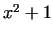 . This choice
behaves nice, though we can not prove this exactly. . This choice
behaves nice, though we can not prove this exactly.
> x[0]:=2: n:=1387: s:=NULL:
> for i from 1 to 8 do x[i]:=x[i-1]^2+1; s:=s,x[i] mod n
> od:
> print(s);
Let us assume, that the number 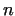 has a non-trivial divisor has a non-trivial divisor 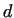 . Considering
the sequence . Considering
the sequence 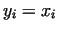 mod mod 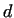 we find, that this sequence will be
eventually periodic (there are only finite different residues mod we find, that this sequence will be
eventually periodic (there are only finite different residues mod 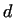 ).
The path of the ).
The path of the 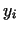 -s draws a greek letter -s draws a greek letter 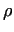 , a tail with a cycle. That
is why this algorithm is called as the Pollard- , a tail with a cycle. That
is why this algorithm is called as the Pollard-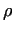 method.
We get method.
We get
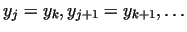 , for some indices , for some indices 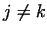 .
Using this .
Using this
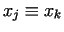 (mod (mod 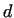 ), i.e. ), i.e. 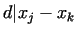 , thus
gcd , thus
gcd
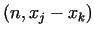 is a non-trivial divisor of is a non-trivial divisor of 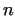 . We do not know the
value . We do not know the
value 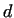 , however if we choose a lot of pairs , however if we choose a lot of pairs 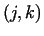 , and compute for the
pairs gcd , and compute for the
pairs gcd
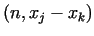 , then usually sooner or later we will find a factor
of , then usually sooner or later we will find a factor
of 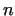 . The efficiency of this algorithm can be improved if we compute
the gcd-s rarer, only for products e.g. 10 pairs of . The efficiency of this algorithm can be improved if we compute
the gcd-s rarer, only for products e.g. 10 pairs of 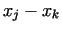 and and 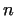 .
To compute integer gcd-s, usually some version of the Euclidean algorithm
(see e.g. in [5])
is used, which is relatively fast.
We illustrate the theoretical description with the factorization of the
number .
To compute integer gcd-s, usually some version of the Euclidean algorithm
(see e.g. in [5])
is used, which is relatively fast.
We illustrate the theoretical description with the factorization of the
number 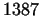 . After finding a divisor we produce the . After finding a divisor we produce the 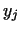 values and
present the " values and
present the "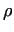 property". property".
> l:=[s]: prod:=1:
> for i from 2 to 8 do prod:=prod*(l[i]-l[i-1]) od:
> prod, igcd(prod,n);
> for i from 1 to 8 do l[i]:=l[i] mod 19 od: l;
> ifactor(1387);
Getting a divisor 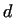 , we check the numbers , we check the numbers 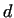 and and 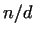 .
If we find that these numbers are not primes, we can try to factorize them
further with the same method or with the basic algorithm.
It is not sure, that the algorithm gives a correct answer.
It is possible, that the gcd is .
If we find that these numbers are not primes, we can try to factorize them
further with the same method or with the basic algorithm.
It is not sure, that the algorithm gives a correct answer.
It is possible, that the gcd is 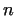 . In this case the
choice for . In this case the
choice for 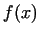 seems to be wrong, let us choose another polynomial seems to be wrong, let us choose another polynomial
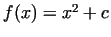 , ,  .
If there is no answer after a long time, then it is better to try another
factorization algorithm.
With Maple we can apply this method to factorize integers, using the function .
If there is no answer after a long time, then it is better to try another
factorization algorithm.
With Maple we can apply this method to factorize integers, using the function
ifactor with the option 'pollard'.
Pollard's  method
Another method of POLLARD is based on the assumption, that the
number method
Another method of POLLARD is based on the assumption, that the
number 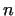 has such a prime factor has such a prime factor 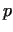 , for which , for which 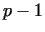 is a product of small
primes. If this happens, then for an arbitrary number is a product of small
primes. If this happens, then for an arbitrary number 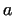 with gcd with gcd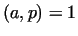 ,
the equation ,
the equation
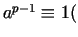 mod mod 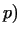 is satisfied.
Thus is satisfied.
Thus 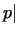 gcd gcd
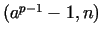 . However, to find this divisor . However, to find this divisor 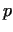 we
have to be lucky. Let us choose a number we
have to be lucky. Let us choose a number
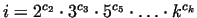 , where
the bases are the first few primes, and the exponents are small positive
integers. After it we compute gcd , where
the bases are the first few primes, and the exponents are small positive
integers. After it we compute gcd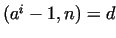 . If . If 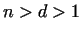 , then
we have found non-trivial factors of , then
we have found non-trivial factors of 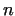 , , 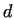 and and 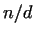 .
If .
If 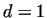 , then we have to choose a larger , then we have to choose a larger 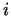 ,
and if ,
and if 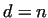 , then we need another base , then we need another base 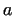 . With this method (called
Pollard . With this method (called
Pollard 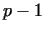 ) we find sometimes very quickly a non-trivial divisor,
but in many cases it does not work. ) we find sometimes very quickly a non-trivial divisor,
but in many cases it does not work.
> n:=973: i:=2^5*3^3*5*7:
> igcd(2^i-1,n);
> ifactor(n);
By combining the basic algorithm with the Pollard methods in most of the
cases we are able to factorize numbers up to roughly 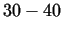 (sometimes (sometimes 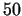 )
decimal digits.
There are some other algorithms, which are suitable for factorization of such
numbers, e.g. a method developed by FERMAT
(see [1] or [8]).
The adventage of his idea is, that this algorithm uses only additions and
substractions, there are no divisions.
However, to a significant improvement we need other approaches. )
decimal digits.
There are some other algorithms, which are suitable for factorization of such
numbers, e.g. a method developed by FERMAT
(see [1] or [8]).
The adventage of his idea is, that this algorithm uses only additions and
substractions, there are no divisions.
However, to a significant improvement we need other approaches.
Sieving algorithms
With the improvement of
FERMAT's original concept we get sieving algorithms ([8]).
In the beginning these methods yield not a significant improvement over 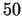 decimal digits. However, in the early
decimal digits. However, in the early 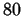 s the quadratic sieve was
discovered, and after a few years with further developments (first of all by
POMERANCE) it proved to be one of the best tools to decompose large
numbers ([1]). In a decade it almost entirely displaced the formerly
successful continued fraction algorithm. s the quadratic sieve was
discovered, and after a few years with further developments (first of all by
POMERANCE) it proved to be one of the best tools to decompose large
numbers ([1]). In a decade it almost entirely displaced the formerly
successful continued fraction algorithm.
An elliptic curve method
Besides the quadratic sieve nowadays the most successful factorization
algorithm is the really surprising elliptic curve method worked out by
H. W. LENSTRA.
In this paper we only outline this method, because the detailed
discussion needs longer introduction to the elliptic curve theory.
Its basic idea is similar to the Pollard 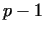 method.
So very briefly,
we choose an elliptic curve in the normal form method.
So very briefly,
we choose an elliptic curve in the normal form
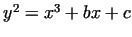 ,
and a number ,
and a number 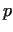 similarly as in the algorithm Pollard similarly as in the algorithm Pollard 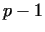 .
We work with a finite group of points (generated by a number .
We work with a finite group of points (generated by a number 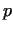 )
on this curve, and compute a gcd.
However, comparing with the Pollard method, if this gcd is 1, then we have
the possibility to choose another ellipitic curve.
Because of the significant difference of the groups (generated by the same
number )
on this curve, and compute a gcd.
However, comparing with the Pollard method, if this gcd is 1, then we have
the possibility to choose another ellipitic curve.
Because of the significant difference of the groups (generated by the same
number 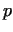 ) on different elliptic curves, sooner or later we have a very
good chance to find a non-trivial divisor
(details in [1] or [12]).
With Maple we can apply this method using the function ) on different elliptic curves, sooner or later we have a very
good chance to find a non-trivial divisor
(details in [1] or [12]).
With Maple we can apply this method using the function
ifactor with the option 'lenstra'.
REMARK
The factorization of large numbers can seem a useless or only theoretically
interesting thing. However, a very important practical application was
discovered in the 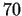 s: a public key crypto-system. The essence of the method
is, that the encrypted message and the key are public, but in spite of this
unauthorized persons are not able to read the message, because to do this
it is needed to factorize a very large number, which is the product of two
large primes (detailed discussion in [1]).
If our "enemy" tries to discover the message, using a s: a public key crypto-system. The essence of the method
is, that the encrypted message and the key are public, but in spite of this
unauthorized persons are not able to read the message, because to do this
it is needed to factorize a very large number, which is the product of two
large primes (detailed discussion in [1]).
If our "enemy" tries to discover the message, using a 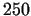 digit key,
it takes years, even if he or she
uses the best current supercomputers and algorithms. digit key,
it takes years, even if he or she
uses the best current supercomputers and algorithms.
| HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-000926-A |  
![[*]](http://heja.szif.hu/Icons/vissza1.gif)
![[*]](http://heja.szif.hu/Icons/elore1.gif) |
|