HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-000926-A |  
![[*]](http://heja.szif.hu/Icons/vissza1.gif)
![[*]](http://heja.szif.hu/Icons/elore1.gif) |
|
With the methods discussed above we can prove very fast - in most of the
cases -, that a number is composite, but usually we are not able to prove
exactly the prime property (even using our best tool, the Miller-Rabin test).
To this we have before this section only the basic algorithm, which is
useless for larger numbers.
Fortunately, we have some other methods which are relatively easy to
programize and are efficient.
We call a number 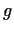 primitive root (mod primitive root (mod 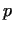 ), if ), if  mod mod 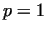 and and
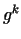 mod mod 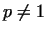 for for 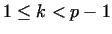 . If there exists a primitive root
(mod . If there exists a primitive root
(mod  ), then ), then 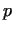 is a prime number, since in this case the numbers is a prime number, since in this case the numbers
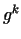 mod mod 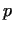 for for
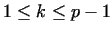 are all different and produce the
numbers are all different and produce the
numbers
 in some order of succession, i.e. in some order of succession, i.e.  does not
have a non-trivial divisor.
The number of the primitive roots (mod does not
have a non-trivial divisor.
The number of the primitive roots (mod 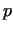 ) is ) is 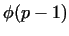 , so it is
relatively easy to find such a number.
For example , so it is
relatively easy to find such a number.
For example 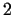 is a primitive root modulo is a primitive root modulo 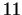 . .
> seq(2^i mod 11,i=1..10);
After finding a number 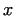 for which for which 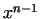 mod mod  , we know already,
that the order of , we know already,
that the order of 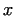 is a divisor of is a divisor of 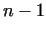 . If the order is exactly . If the order is exactly  ,
then ,
then 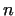 is prime. So we have to check the exponents, which are the (prime)
divisors of is prime. So we have to check the exponents, which are the (prime)
divisors of 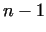 , namely the exponents , namely the exponents  .
Thus, by the check of the following two conditions we have a very nice method
to prove exactly the prime property:
a) .
Thus, by the check of the following two conditions we have a very nice method
to prove exactly the prime property:
a)  mod mod 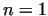 ,
b) ,
b) 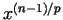 mod mod 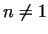 , for all prime divisors , for all prime divisors 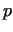 of of  .
It is known moreover, that the .
It is known moreover, that the 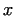 bases here are allowed to be different,
the prime property is still satisfied (J. BRILLHART, D. H. LEHMER and
J. L. SELFRIDGE, 1975), details in [1].
Thus to prove the prime property of bases here are allowed to be different,
the prime property is still satisfied (J. BRILLHART, D. H. LEHMER and
J. L. SELFRIDGE, 1975), details in [1].
Thus to prove the prime property of
 , we need the complete factorization of , we need the complete factorization of 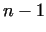 . However in many cases we
are not able to factorize . However in many cases we
are not able to factorize 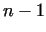 , if , if 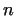 is very large.
That is, why perfected methods were worked out, using only the
partial factorization of is very large.
That is, why perfected methods were worked out, using only the
partial factorization of 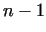 or that of or that of 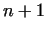 .
In the first case let us write .
In the first case let us write 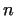 in the form in the form
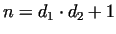 , where , where
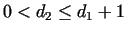 .
If for all prime divisor .
If for all prime divisor 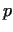 of of 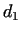 there exists an there exists an 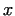 ,
for which ,
for which  mod mod 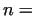 gcd gcd
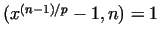 , then , then  is prime
(H. C. POCKLINGTON, 1914).
We use these two methods in the following subsection to prove the prime
property of a large number.
Similarly as by the factorization, there are exact prime tests using elliptic
curves (details in [1]).
Moreover, very effective methods are known to prove the prime properties of
numbers in special forms, e.g. for Fermat numbers and Mersenne numbers.
These methods start so, that we know the factorization of is prime
(H. C. POCKLINGTON, 1914).
We use these two methods in the following subsection to prove the prime
property of a large number.
Similarly as by the factorization, there are exact prime tests using elliptic
curves (details in [1]).
Moreover, very effective methods are known to prove the prime properties of
numbers in special forms, e.g. for Fermat numbers and Mersenne numbers.
These methods start so, that we know the factorization of 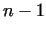 or or 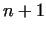 , but
they use further special improvements.
The following test for Mersenne numbers was worked out by É. LUCAS
and D. H. LEHMER (proof in [8]).
Let , but
they use further special improvements.
The following test for Mersenne numbers was worked out by É. LUCAS
and D. H. LEHMER (proof in [8]).
Let 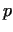 be an odd prime, and let us define the sequence be an odd prime, and let us define the sequence  in the
following manner: in the
following manner:
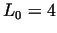 , ,
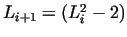 mod mod 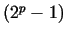 .
Then .
Then 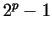 is prime if and only if is prime if and only if 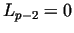 .
Due to this method, we are able to prove the prime property of very large
Mersenne numbers. Here we check the .
Due to this method, we are able to prove the prime property of very large
Mersenne numbers. Here we check the 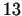 th Mersenne number. th Mersenne number.
> L:=4: l:=4: m:=13:
> for i from 1 to m-2 do
> L:=(L*L - 2) mod (2^m-1): l:=l,L
> od: l;
| HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-000926-A |  
![[*]](http://heja.szif.hu/Icons/vissza1.gif)
![[*]](http://heja.szif.hu/Icons/elore1.gif) |
|