|
Problem: Let 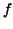 be a positive valued (bounded) function on a closed (finite) interval be a positive valued (bounded) function on a closed (finite) interval ![$[a,b]$](img2.gif) of the real numbers. Compute the area of the region in the of the real numbers. Compute the area of the region in the 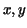 plane bounded by the graph of plane bounded by the graph of  , the , the  -axis and the straight lines -axis and the straight lines 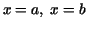 . .
EXAMPLE 1.1.
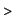 f:=x->x*sin(x)^2;
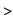 plot(f(x),x=1..3,y=0..2,scaling=CONSTRAINED);
For ``general'' functions this looks like a hard problem. However, for
some types of special functions (e.g. linear functions) the problem is
easy. Let us look at stepfunctions. A stepfunction 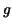 on on ![$[a,b]$](img12.gif) is given by a subdivision of
is given by a subdivision of
![$[a,b]$](img13.gif) , i.e. a finite sequence of numbers , i.e. a finite sequence of numbers
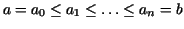 and function values and function values
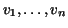 such that such that 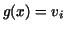 for all for all 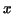 such that such that
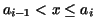 for all for all 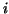 , whereas , whereas  for all for all  and and 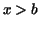 . .
Since stepfunctions play an important role we introduce the procedure
stepfunction to produce them. It has two arguments, a subdivision 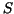 and a list of function values
and a list of function values 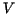 . With the notations above . With the notations above
![$S=[a_{0},\ldots,a_{n}]$](img25.gif) and and
![$V=[v_{1},\ldots,v_{n}]$](img26.gif) . .
EXAMPLE 1.2.
 S:=[3,3.7,5,6.2,7.1,8]: V:=[2.5,-1,4.2,3,-2]:
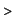 g:=stepfunction(S,V):
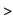 plot(g,x=0..10,scaling=CONSTRAINED);
For positive stepfunctions the solution to the area problem
is immediate and given by the formula
Note that this formula makes sense for general stepfunctions: the
resulting number represents the area above the  -axis minus the area
below the -axis minus the area
below the 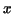 -axis. The procedure int_step yields the above sum for
given -axis. The procedure int_step yields the above sum for
given  and and 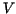 . .
EXAMPLE 1.3.
For the stepfunction  in Example 1.2. the area
under the graph of in Example 1.2. the area
under the graph of 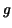 is is
 int_step(S,V);
Now back to the problem for general functions. The idea is to
approximate such a function 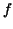 by stepfunctions. E.g.,
a continuous function can be well approximated with constant on sufficiently small intervals. Let us look at the function by stepfunctions. E.g.,
a continuous function can be well approximated with constant on sufficiently small intervals. Let us look at the function 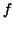 of Example 1.1. of Example 1.1.
EXAMPLE 1.4.
Take a regular subdivision of ![$[a,b]$](img42.gif) , i.e. a subdivision into , i.e. a subdivision into
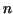 subintervals of equal length. subintervals of equal length.
 f:=x->x*sin(x)^2:
 n:=10:
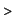 S:=[seq(1.+2*`i`/n,`i`=0..n)];
For the value of the stepfunction on
![$[a_{i - 1},a_{i}]$](img48.gif) we choose we choose 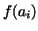 .
Hence .
Hence
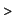 V:=[seq(f(S[`i`]),`i`=2..n+1)];
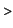 g:=stepfunction(S,V):
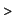 plot(\{f(x),g(x)\},x=1..3);
This plot shows the function 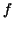 and its approximating
stepfunction and its approximating
stepfunction 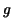 . Some daemon (in fact Maple's
procedure int) tells us that the area under the graph of . Some daemon (in fact Maple's
procedure int) tells us that the area under the graph of 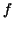 equals to
equals to 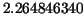 whereas the area under the
graph of whereas the area under the
graph of 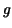 is given by is given by
 int_step(S,V);
which can be rounded to 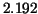 . Neither very good nor totally bad as an
approximation. We can get a better approximation by increasing the
number of subintervals: . Neither very good nor totally bad as an
approximation. We can get a better approximation by increasing the
number of subintervals:
 n:=50: S:=[seq(1.+2*`i`/n,`i`=0..n)]:
 V:=[seq(f(S[`i`]),`i`=2..n+1)]:
 g:=stepfunction(S,V):
 plot(\{f(x),g(x)\},x=1..3,numpoints=500); g:='g':
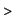 int_step(S,V);
rounded to  , a much better approximation. , a much better approximation.
Exercise 1.1.
Consider the function
The region under the graph of 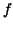 between between 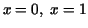 is a is a  degree
circle sector. Hence the area equals to degree
circle sector. Hence the area equals to 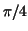 . Use the above method of approximation by regular
stepfunctions to find an approximation of . Use the above method of approximation by regular
stepfunctions to find an approximation of 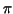 . How many subintervals are needed to approximate . How many subintervals are needed to approximate 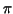 with an error less then or equal to with an error less then or equal to 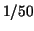 ? ?
The Maple package ``student'' contains the functions leftsum and
rightsum, which are in case of regular subdivision the same as
the function int_step. I.e., the function leftsum (rightsum) computes a numerical approximation to a definite integral using rectangles. The
height of each rectangle is determined by the value of the function at
the left (right) side of each subinterval. A graph of the
approximation can be obtained by the Maple procedure leftbox
(rightbox).
Exercise 1.2.
Approximate the function
on the intarval ![$[4,6]$](img80.gif) by regular stepfunctions using the procedure
with an error less than by regular stepfunctions using the procedure
with an error less than  . How many subintervals were needed in
each case? . How many subintervals were needed in
each case?
| 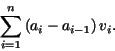
![\begin{eqnarray*}
\lefteqn{S := [1., \,1.200000000, \,1.400000000, \,1.600000000...
...00000, \,2.600000000, \,2.800000000, \,3.]
\mbox{\hspace{178pt}}
\end{eqnarray*}](img47.gif)
![\begin{eqnarray*}
\lefteqn{V := [1.042436229, \,1.359555639, \,1.598635820, \,
1...
....6909283272, \,.3142077702, \,
.05974457007]\mbox{\hspace{20pt}}
\end{eqnarray*}](img51.gif)
![\includegraphics[width=12cm]{int01.ps}](img10.gif)
![\includegraphics[width=12cm]{int02.ps}](img30.gif)
![\includegraphics[width=12cm]{int03.ps}](img54.gif)
![\includegraphics[width=12cm]{int04.ps}](img67.gif)