|
For a bounded function 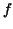 on a (finite) interval on a (finite) interval
![$[a,b]$](img83.gif) and a subdivision and a subdivision 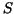 of of ![$[a,b]$](img85.gif) one can define two special
stepfunctions: one can define two special
stepfunctions: 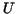 and and 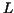 (upper and lower stepfunction) as follows. (upper and lower stepfunction) as follows.
Let
![$S:=[a_{0},\ldots,a_{n}]$](img88.gif) . Then for all . Then for all
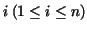 and and 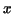 satisfying
satisfying
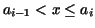 one puts one puts
and
respectively.
EXAMPLE 2.1. (cf. EXAMPLE 1.4.)
 f:=x->x*sin(x)^2: n:=10: S:=[seq(1.+2*`i`/n,`i`=0..n)]:
 integral_plot(f,S,'riemann');
5
By definition the graph of  lies below that of lies below that of 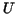 and above the one of
and above the one of 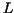 . Hence the area . Hence the area 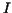 below the graph of below the graph of
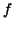 must satisfy must satisfy
Here lower (resp. upper) is the area
under the graph of 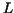 (resp. (resp.  ). In our example it means the values ). In our example it means the values
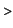 lower(f,S);
 upper(f,S);
If we make the subdivision finer and finer the approximation of 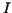 by upper and lower should be better and better. by upper and lower should be better and better.
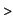 n:=25: S:=[seq(1.+2*`i`/n,`i`=0..n)]:
 integral_plot(f,S,'riemann');
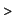 lower(f,S);
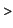 upper(f,S);
Let us denote the subdivision 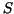 devided into devided into 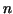 subintervals by subintervals by 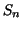 . Now we must realize that ``the area under the graph of . Now we must realize that ``the area under the graph of 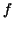 ''
has never been properly defined (though it is a
very intuitive notion). The notions introduced here, however, give a
good opportunity. ''
has never been properly defined (though it is a
very intuitive notion). The notions introduced here, however, give a
good opportunity.
- Definition:
 is called (Riemann-)
integrable if there exists a real number is called (Riemann-)
integrable if there exists a real number 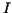 such that such that
The number  is called the ``integral of is called the ``integral of 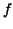 over over ![$[a,b]$](img126.gif) ''. ''.
- Notations:
-
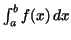 commonly or sometimes in text form commonly or sometimes in text form
int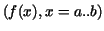 . .
Subsections
| ![\includegraphics[width=12cm]{int05.ps}](img96.gif)
![\includegraphics[width=12cm]{int06.ps}](img112.gif)