Submitted to HEJ
Manuscript no.: ANM-010201-A
|  

 |
|
For many purposes it is important to be able to calculate areas using
polar coordinates. Let 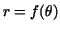 be the equation of a curve in polar coordinates. Let be the equation of a curve in polar coordinates. Let  be the area
of the region which is bounded by the be the area
of the region which is bounded by the 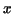 -axis (that is, the line -axis (that is, the line
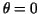 ), the line through the origin making an angle ), the line through the origin making an angle  with the
with the 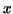 -axis, and the portion of the curve between these two
lines. By the fundamental theorem of the integral calculus, the area
of the sector between the polar angles -axis, and the portion of the curve between these two
lines. By the fundamental theorem of the integral calculus, the area
of the sector between the polar angles 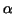 and and  is given by the expression is given by the expression
If 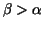 , this expression cannot be less than zero. , this expression cannot be less than zero.
EXAMPLE 7.2.
Consider the area bounded by the one loop of a lemniscate. The
equation of the lemniscate is
 ,
and we obtain one loop by letting ,
and we obtain one loop by letting 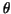 vary from vary from
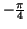 to to
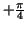 . The shape of one loop of the lemniscate with . The shape of one loop of the lemniscate with 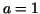 is is
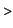 plot([2*cos(2*theta),theta,theta=-Pi/4..Pi/4],coords=polar);
The area of the loop in general is
 a^2*Int(cos(2*theta),theta=-Pi/4..Pi/4);
We find that the value of the integral is
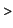 value(%);
| Submitted to HEJ
Manuscript no.: ANM-010201-A
|  

 |
|
![\includegraphics[width=12cm]{int13.ps}](img552.gif)