Submitted to HEJ Manuscript no.: ANM-010201-A

How the computer works?

The method applied in the two preceding exercises is not obvious. There are many more methods for computing primitives of special classes of functions. Until recently the computation of primitives of elementary functions (an elementary function is traditionally meant to be an element of the set of functions that can be built up recursively by starting from $\mbox {\ms Q}(x)$ and taking sums, products, quotients, logarithms, exponentials, algebraic functions and compositions of them) came down to skillfully applying a whole ``bag of tricks''. This has been so for centuries and many great mathematicians have been occupied with this problem. A practical approach consists of making integral tables, large collections of functions and their primitives. Only since the fundamental work of Robert Risch we dispose of an algorithm which decides whether the primitive of an elementary function is again an elementary function, and if it is, it will be computed. His algorithm is (partly) implemented in the bigger computer algebra systems (like Maple). It is too complicated to explain here. However, because of the Risch algorithm there is less need of exercises with the bag of tricks. So we shall not dive into integration methods for special classes of functions. Instead some examples of Maple's int procedure will be shown.

EXAMPLE 4.1.

$>$ Int(1/sqrt(3-2*x-x^2),x);

$${\displaystyle \int } {\displaystyle \frac {1}{\sqrt{3 - 2\,x - x ^{2}}}} \,dx$$

$>$ value(%);

$${\rm arcsin}({\displaystyle \frac {1}{2}} + {\displaystyle \frac {1}{2}} \,x)$$

Check by differentiating!

EXAMPLE 4.2.

$>$ Int(sin(x)^2*cos(x)^5,x);

$${\displaystyle \int } {\rm sin}(x)^{2}\,{\rm cos}(x)^{5}\,dx$$

$>$ value(%);

$$- {\displaystyle \frac {1}{7}} \,{\rm sin}(x)\,{\rm cos}(x)... ...,{\rm sin}(x ) + {\displaystyle \frac {8}{105}} \,{\rm sin}(x)$$

EXAMPLE 4.3.

$>$ Int((2*x^3-2*x^2-1)/(x-1)^2*exp(x^2),x);

$${\displaystyle \int } {\displaystyle \frac {(2\,x^{3} - 2\,x^{2} - 1)\,e^{(x^{2})}}{(x - 1)^{2}}} \,dx$$

$>$ value(%);

$${\displaystyle \frac {x\,e^{(x^{2})}}{x - 1}}$$

Now let us see how Maple is working when computing such integrals.

$>$ infolevel[int]:=2:

$>$ Int((-exp(x)-x+ln(x)*x+ln(x)*x*exp(x))/(x*(exp(x)+x)^2),x);

$${\displaystyle \int } {\displaystyle \frac { - e^{x} - x + {\rm ln}(x)\,x + {\rm ln}(x)\,x\,e^{x}}{x\,(e^{x} + x)^{2}}} \,dx$$

$>$ value(%);

$>$ infolevel[int]:=0:

int/indef: first-stage indefinite integration
int/indef2: second-stage indefinite integration
int/indef2: trying integration by parts
int/rischnorm: enter Risch-Norman integrator
int/risch: enter Risch integration
int/risch/algebraic1: RootOfs should be algebraic numbers and functions
int/risch: the field extensions are

$$[{\it\_X}, \,e^{{\it\_X}}, \,{\rm ln}({\it\_X})]$$

int/risch: Introduce the namings:

$$\{{{\it\_th}_{1}}=e^{{\it\_X}}, \,{{\it\_th}_{2}}={\rm ln}( {\it\_X})\}$$

unknown: integrand is

$${\displaystyle \frac { - {{\it\_th}_{1}} - {\it\_X} + {\it\_... ...{\it\_th}_{1} }}{{\it\_X}\,({{\it\_th}_{1}} + {\it\_X})^{2}}}$$

int/risch/logpoly: integrating

$${\displaystyle \frac { - {{\it\_th}_{1}} - {\it\_X} + {\it\_... ...{\it\_th}_{1} }}{{\it\_X}\,({{\it\_th}_{1}} + {\it\_X})^{2}}}$$

int/risch/int: integrand is

$${\displaystyle \frac {1 + {{\it\_th}_{1}}}{({{\it\_th}_{1}} + {\it\_X})^{2}}}$$

int/risch/ratpart: integrating

$${\displaystyle \frac {1 + {{\it\_th}_{1}}}{({{\it\_th}_{1}} + {\it\_X})^{2}}}$$

int/risch/ratpart: Hermite reduction yields

$$- {\displaystyle \frac {1}{{{\it\_th}_{1}} + {\it\_X}}} + {\displaystyle \int } 0\,d{\it\_X}$$

int/risch/int: integrand is

$$0$$

int/risch/int: integrand is

$$0$$

int/risch/logpoly: result is

$$- {\displaystyle \frac {{{\it\_th}_{2}}}{{{\it\_th}_{1}} + {\it\_X}}}$$

int/risch: exit Risch integration

$$- {\displaystyle \frac {{\rm ln}(x)}{e^{x} + x}}$$

What we have seen? At the first stage of the integration routine Maple tries to simplify the problem by applying the known integration rules for polynomials (rule (e) in section 2.). Next, (as any calculus student would) tries to integrate using simple table lookup processes. Then looks for other specific types of intergrands and uses appropriate methods: integration by part technique, possible substitutions (here called derivative-devides method). This heuristic method used by Maple obtains the correct answer for a suprisingly large percentage of integral problems. (And even very quickly). If the heuristic part fails then the problem is converted into the exp-log notation and a finite decision procedure is invoked. The result of the latter procedure will be either the integral expressed in the exp-log notation or an indication that could not find the elementary integral in which cases $\int f(x)\,dx$ returns itself. Does it mean that the elementary integral does not exist? Not by all means. In such cases some very elementary trick could help.

EXAMPLE 4.4. -- Don't trust Maple's integrator too much.

$>$ f:=x->log(x+sqrt(x^2+1));

$$f := x\rightarrow {\rm log}(x + \sqrt{x^{2} + 1})$$

$>$ Int(f(x),x);

$${\displaystyle \int } {\rm ln}(x + \sqrt{x^{2} + 1})\,dx$$

$>$ value(%);

$${\displaystyle \int } {\rm ln}(x + \sqrt{x^{2} + 1})\,dx$$

Would it mean that the result is not an elementary function? Putting

$$f(x)={\rm ln}(x + \sqrt{x^{2} + 1}),$$

the partial integration yields

$>$ Int(f(x),x) = x*f(x)-Int(x*diff(f(x),x),x);

$${\displaystyle \int } {\rm ln}(x + \sqrt{x^{2} + 1})\,dx=x\,... ...e \frac {x}{\sqrt{x^{2} + 1}}} )}{x + \sqrt{x^{2} + 1}}} \,dx$$

$>$ value(%);

$${\displaystyle \int } {\rm ln}(x + \sqrt{x^{2} + 1})\,dx=x\,{\rm ln}(x + \sqrt{x^{2} + 1}) - \sqrt{x^{2} + 1}.$$

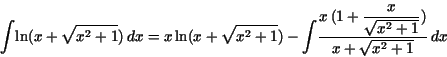
Exercise 4.1.

Compute $\int e^{{\rm arcsin}(x)}\,dx$.

Submitted to HEJ Manuscript no.: ANM-010201-A