|
Let us recall the so-called fundamental theorem of calculus.
- Theorem 1.
- Let
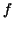 be a continuous function on the interval be a continuous function on the interval ![$[a,b]$](img185.gif) .
For any .
For any ![$c\in [a,b]$](img186.gif) define define
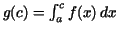 .
Then .
Then
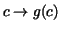 is a differentiable function on is a differentiable function on ![$[a,b]$](img189.gif) and and
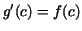 for all for all ![$c \in [a,b]$](img191.gif) . .
This theorem is extremely useful. Because if we have to compute the value
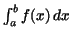 and we are so fortunate to find a function
and we are so fortunate to find a function 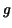 such that such that 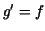 , then , then
Such a function 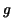 is called a primitive of is called a primitive of 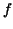 (or anti-derivative of (or anti-derivative of 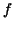 , indefinite integral of , indefinite integral of 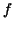 ). ). 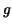 is determined up to an
additive constant. The usual notation for is determined up to an
additive constant. The usual notation for 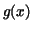 is is
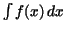 .
Now we can compute immediately lots of integrals: .
Now we can compute immediately lots of integrals:
EXAMPLE 3.1.
 Int(3*x^2-5*x^7,x=3..5);
In order to compute this integral we must find a function 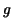 such that such that
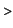 diff(g(x),x)=3*x^2-5*x^7;
One sees immediately that
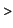 g:=x->x^3-5/8*x^8;
is such a function. And so
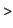 Int(3*x^2-5*x^7,x=3..5)=g(5)-g(3); g:='g':
EXAMPLE 3.2.
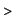 Int(2*x*exp(x^2),x=1..2);
We must find a function 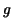 such that such that
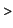 diff(g(x),x)=2*x*exp(x^2);
Here we are ``fortunate'' again, because one sees at once that
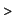 g:=x->exp(x^2);
will do. So we find
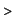 Int(x*exp(x^2),x=1..2)=g(2)-g(1);
Apply evalf if you want a numerical result,
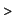 evalf(g(2)-g(1)); g:='g':
EXAMPLE 3.3.
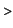 Int(ln(x)^2,x);
Now we should find  such that such that
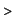 diff(g(x),x)=ln(x)^2;
This is a bit harder. However, we can proceed as follows. We can find
a  which is almost OK: which is almost OK:
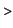 g:=x->x*ln(x)^2;
Then
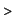 diff(g(x),x);
In this expression we should get rid of the term 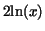 . So if we
can find a function . So if we
can find a function 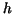 satisfying satisfying
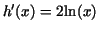 , we are done, because then we can replace , we are done, because then we can replace 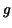 by by 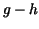 . So we are reduced to a
similar, but simpler problem. A candidate for . So we are reduced to a
similar, but simpler problem. A candidate for 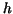 is
given by is
given by
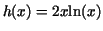 . Then . Then
 . Now we must get rid of the term . Now we must get rid of the term 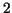 . This is easy: replace . This is easy: replace 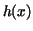 by by 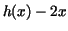 : :
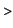 h:=x->2*x*ln(x)-2*x;
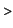 diff(h(x),x);
This is what we were looking for. Hence our 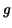 becomes becomes
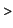 g:=x->(x*ln(x)^2-(2*x*ln(x)-2*x));
Check:
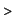 diff(g(x),x);
The trick applied twice in the latter example is the so-called
integration by parts which can be expressed by the following
formula
This is valid for continuously differentiable functions 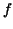 and
and 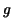 . The proof is by differentiation. . The proof is by differentiation.
Exercise 3.1.
Compute the primitives of the following functions. Check the results by
differentiating:
Exercise 3.2. (cf. EXAMPLE 1.4.)
Compute
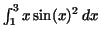 . .
Hint: use the relation
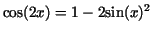 . .
EXAMPLE 3.4.
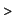 Int(1/(x*ln(x)),x);
(restricted to 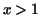 ). Here integration by parts seems
powerless. In textbooks you may find: ). Here integration by parts seems
powerless. In textbooks you may find:
The first relation makes sense when one applies the thumb rule:
 ; the second one by putting ln ; the second one by putting ln , namely , namely
and substituting by  . This juggling can be turned into a
precise theorem: . This juggling can be turned into a
precise theorem:
- Theorem 2.
- (``Substitution rule'') Let
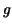 be a continuously
differentiable function on be a continuously
differentiable function on ![$[a,b]$](img270.gif) and and  a continuous function defined
for all a continuous function defined
for all 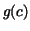 where where ![$c\in [a,b]$](img273.gif) . Then . Then
for all ![$y \in [a,b]$](img275.gif) . .
The proof of this useful theorem is very simple: differentiate both
sides of the formula with respect to 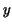 . Then one gets an equality. So
both members differ by a constant (i.e. independent of . Then one gets an equality. So
both members differ by a constant (i.e. independent of 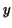 ). Finally,
substitute ). Finally,
substitute 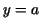 . Often the substitution rule is written in a less
careful way: . Often the substitution rule is written in a less
careful way:
Example 3.4. now goes as follows: let
and
Then
and
Hence we find
EXAMPLE 3.5.
 Int(1/sqrt(1-x^2),x);
Here the substitution 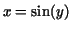 is helpful. To be a bit more precise the function is helpful. To be a bit more precise the function
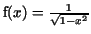 is defined and it is greater than is defined and it is greater than 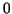 for for 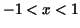 and and 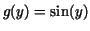 is restricted to is restricted to 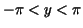 . Then . Then
because  for the values of for the values of 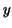 under consideration.
Since under consideration.
Since  the substitution formula yields the substitution formula yields
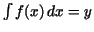 .
Obviously, we want .
Obviously, we want  as a function of as a function of 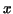 . This is easy: . This is easy:
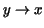 is the inverse function arcsin of sin. Hence is the inverse function arcsin of sin. Hence
Exercise 3.3.
Compute
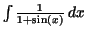 and check your result by differentiating. and check your result by differentiating.
Hint: substitute
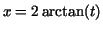 . First show that . First show that
The substitution rule now shows that our integral is replaced by
 where where 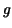 is a rational function of is a rational function of 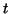 . .
Remark: This method works for any integral of the form
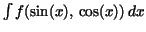 , where , where 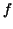 is rational function of two variables. is rational function of two variables.
Exercise 3.4.
Compute
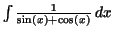 . .
|