HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-980205-A
| 

 |
|
The preconditioned conjugate gradient (PCG) based domain decomposition
methods are intensively investigated parallel algorithms for the
numerical solution of elliptic problems. Numerous papers are devoted to this
topic, see for example
[1,2,3,4,5,7].
Several Schur complement preconditioner constructions are an appropriate matrix
representation of the 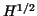 seminorm [1,7].
In this paper we give a new explicit circulant representation of the seminorm [1,7].
In this paper we give a new explicit circulant representation of the 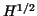 seminorm in the space of bilinear finite elements defined on the surface of the
unit cube
seminorm in the space of bilinear finite elements defined on the surface of the
unit cube
![\begin{displaymath}
U = [0,1]^3.
\end{displaymath}](img4.gif) |
(1) |
Our construction is based on the separability property of the 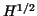 seminorm
on rectangules and an application of a sparse matrix representation
[6] of the one-dimensional seminorm
on rectangules and an application of a sparse matrix representation
[6] of the one-dimensional 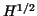 seminorm in the space of linear
finite elements.
The given construction can be generalized in a straightforward way to more
complicated cases, for example complex domains that are unions of
rectangular elements. seminorm in the space of linear
finite elements.
The given construction can be generalized in a straightforward way to more
complicated cases, for example complex domains that are unions of
rectangular elements.
This paper is organised as follows.
The separability property of the 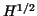 seminorm on a rectangular shaped
surface is discussed in Section 2.
Section 3 contains the description of a representation of the 'partial'
seminorms by a sum of one-dimensional seminorms
in the space of bilinear finite elements.
The circulant matrix representation
of the seminorm on a rectangular shaped
surface is discussed in Section 2.
Section 3 contains the description of a representation of the 'partial'
seminorms by a sum of one-dimensional seminorms
in the space of bilinear finite elements.
The circulant matrix representation
of the 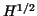 seminorm on the surface of seminorm on the surface of 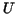 (1) is described in Section 4.
Numerical results regarding to this representation are given in Section 5. (1) is described in Section 4.
Numerical results regarding to this representation are given in Section 5.
| HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-980205-A
| 

 |
|