HEJ, HU ISSN 1418-7108 Manuscript no.: ANM-980205-A

The Separability Property

The $H^{1/2}$ seminorm on

$$Q = [0,a] \times [0,b]$$ (2)

can be defined by the formula [8]

$$\mid f \mid^2_{H^{1/2}(Q)} = \int_0^a \int_0^b \int_0^a \i... ... \mid^2 + \mid x_2 - y_2 \mid^2 )^{3/2}} dy_2 dy_1 dx_2 dx_1$$ (3)

and the separability property can be formulated az follows.

Theorem 2.1   Let $f \in H^{1/2}(Q)$. Then

$$2^{-3}({1-\frac{max \{a^2,b^2\}}{(a+b)^2}}) (\mid f \mid^2_{H_a^{1/2}(Q)}+\mid f \mid^2_{H_b^{1/2}(Q)}) \le$$

$$\le \quad \mid f \mid^2_{H^{1/2}(Q)} \quad \le$$ (4)

$$\le 2^{5/2} (\mid f \mid^2_{H_a^{1/2}(Q)}+\mid f \mid^2_{H_b^{1/2}(Q)}),$$

where

$$\mid f \mid^2_{H_a^{1/2}(Q)} = \int_0^a \int_0^b \int_0^b ... ... - f(x_1,y_2) \mid^2} {\mid x_2 -y_2 \mid^2} dy_2 dx_2 dx_1$$ (5)

and

$$\mid f \mid^2_{H_b^{1/2}(Q)} = \int_0^b \int_0^a \int_0^a ... ... - f(y_1,x_2) \mid^2} {\mid x_1 -y_1 \mid^2} dy_1 dx_1 dx_2$$ (6)

are the 'partial' seminorms.

The proof of this theorem is divided into several steps by the Lemmata 2.2-2.5.

Lemma 2.2  

$$c^2+d^2 \le (c+d)^2 \le 2c^2+2d^2, \quad \forall c,d \in [0,\infty)$$ (7)

$$\frac{1}{(c+d)^3} \le \frac{1}{(c^2+d^2)^{3/2}} \le 2^{3/2} \frac{1}{(c+d)^3}, \quad \forall c,d \in (0,\infty)$$ (8)

$$(c-d)^2 = 2^2 (c-\frac{c+d}{2})^2 = 2^2 (d-\frac{c+d}{2})^2, \quad \forall c,d \in (-\infty,\infty)$$ (9)

The inequalities of this lemma can be verified by simple calculation.

Lemma 2.3   Let $c,d \in (0,\infty)$. Then

$$\frac{1}{2}({1-{\frac{d^2}{(c+d)^2}}}) \frac{1}{y^2} \le \... ... \frac{1}{(y+\mid t-x \mid)^3}dt = g(x,y) \le \frac{1}{y^2},$$ (10)

$$x \in [0,c], y \in (0,d].$$

Proof 2.4   A simple calculation gives

$$g(x,y) = \frac{1}{y^2} - \frac{1}{2}({\frac{1}{(y+x)^2}+\frac{1}{(y+c-x)^2}}), \quad x \in [0,c], y \in (0,d].$$

For every fixed $y$ the possible points of extremal values in the interval $(0,c)$ are given by the solution of the $\frac{\partial g}{\partial x}(x,y) = 0$ equation. By a standard calculation one can get, that $x=\frac{c}{2}$ is the unique extremal point and it is a local maximum. Therefore the function $g(x,y)$ can reach its minimum values at the endpoints of the $[0,c]$ interval. Because of

$$g(0,y) = g(c,y) = \frac{1}{2}({\frac{1}{y^2}-\frac{1}{(c+y)^2}})$$

we can write

$$\frac{1}{2} ({1 - \frac{d^2}{(c+d)^2}}) \frac{1}{y^2} \le g(... ...,y) = \frac{1}{y^2} - \frac{1}{({c/2}+y)^2} \le \frac{1}{y^2}$$

and this completes the proof.

Lemma 2.5   Let $f \in H^{1/2}(Q)$. Then

$$2^{-2}({1 - \frac{b^2}{(a+b)^2}})\mid f \mid^2_{H_a^{1/2}(Q)} \le \mid f \mid^2_{H^{1/2}(Q)},$$ (11)

$$\quad 2^{-2}({1 - \frac{a^2}{(a+b)^2}})\mid f \mid^2_{H_b^{1/2}(Q)} \le \mid f \mid^2_{H^{1/2}(Q)}.$$ (12)

Proof 2.6   Let us consider Lemma 2.3 with $c = a$, $d = b$ $y = \mid x_2 - y_2 \mid$, $x=x_1$ and $t=y_1$. Then we get

$$\frac{1}{2}({1 - \frac{b^2}{(a+b)^2}})\frac{1}{\mid x_2 - y_2... ...^a \frac{1}{({\mid x_2 -y_2 \mid + \mid x_1 -y_1 \mid})^3}dy_1.$$

Hence

$$\frac{1}{2}({1 - \frac{b^2}{(a+b)^2}}) \mid f \mid^2_{H_a^{1/2}(Q)} \le$$

$$\le \int_0^a \int_0^b \int_0^b \int_0^a \frac{\mid f(x_1,x_2... ..._2 \mid + \mid x_1 -y_1 \mid})^3} dy_1 dy_2 dx_2 dx_1 = I_1.$$

From (8) of Lemma 2.2 with $c = \mid x_2 - y_2 \mid$ and $d = \mid x_1 - y_1 \mid$ we obtain

$$I_1 \le \int_0^a \int_0^b \int_0^b \int_0^a \frac{\mid f(x_... ...d^2 + \mid x_1 -y_1 \mid^2})^{3/2}} dy_1 dy_2 dx_2 dx_1 = I_2.$$

Using the Fubini's theorem, (7) and (9) of Lemma 2.2

$$I_2 \le \frac{1}{4} \int_0^a \int_0^b \int_0^a \int_0^b ... ..._2 - \frac{x_2+y_2}{2} \mid^2})^{3/2}} dy_2 dy_1 dx_2 dx_1 +$$

$$+ \frac{1}{4} \int_0^a \int_0^b \int_0^a \int_0^b \frac{\m... ...\frac{x_2+y_2}{2} \mid^2})^{3/2}} dx_2 dy_1 dy_2 dx_1 = I_3.$$

By the substitutions $t_1 = \frac{x_1+y_1}{2}$ and $t_2 = \frac{x_2+y_2}{2}$ we have

$$I_3 = \int_0^a \int_0^b \int_{\frac{x_1}{2}}^{\frac{a+x_1... ...mid^2 + \mid x_2 - t_2 \mid^2})^{3/2}} dt_2 dt_1 dx_2 dx_1 +$$

$$+ \int_0^a \int_0^b \int_{\frac{x_1}{2}}^{\frac{a+x_1}{2}} ... ...^2 + \mid y_2 - t_2 \mid^2})^{3/2}} dt_2 dt_1 dy_2 dx_1 \le$$

$$\le 2 \int_0^a \int_0^b \int_0^a \int_0^b \frac{\mid f(r_1,... ...\mid^2 + \mid r_2 - s_2 \mid^2})^{3/2}} ds_2 ds_1 dr_2 dr_1.$$

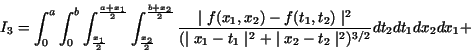
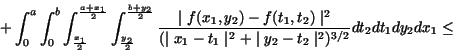
Since the four integrals on the right hand side are the definition of $\mid f \mid^2_{H^{1/2}(Q)}$ the estimation is proved. The inequality (12) can be proved analogously.

Lemma 2.7   Let $f \in H^{1/2}(Q)$. Then

$$\mid f \mid^2_{H^{1/2}(Q)} \le 2^{5/2} (\mid f \mid^2_{H_a^{1/2}(Q)}+\mid f \mid^2_{H_b^{1/2}(Q)})$$ (13)

Proof 2.8   Using (7) of Lemma 2.2 we obtain

$$\mid f \mid^2_{H^{1/2}(Q)} = \int_0^a \int_0^b \int_0^a \int... ...id^2 + \mid x_2 - y_2 \mid^2})^{3/2}} dy_2 dy_1 dx_2 dx_1 \le$$

$$\le 2\int_0^a \int_0^b \int_0^a \int_0^b \frac{\mid f(x_1,x_... ...\mid^2 + \mid x_2 - y_2 \mid^2})^{3/2}} dy_2 dy_1 dx_2 dx_1 +$$

$$+ 2\int_0^a \int_0^b \int_0^a \int_0^b \frac{\mid f(x_1,y_2)... ...\mid^2 + \mid x_2 - y_2 \mid^2})^{3/2}} dy_2 dy_1 dx_2 dx_1 =$$

$$= 2I_1+2I_2.$$

Hence it is enough to show that

$$I_1 \le 2^{3/2}\mid f \mid^2_{H_a^{1/2}(Q)} \mbox{ and } I_2 \le 2^{3/2}\mid f \mid^2_{H_b^{1/2}(Q)}.$$

Let us consider (8) of Lemma 2.2 with $c=\mid x_1 -y_1 \mid$ and $d=\mid x_2 -y_2 \mid$. Then we get

$$I_1 \le 2^{3/2} \int_0^a \int_0^b \int_0^a \int_0^b \frac{\... ... \mid x_2 - y_2 \mid})^{3}} dy_2 dy_1 dx_2 dx_1 = 2^{3/2}J_1.$$

Due to the Fubini's theorem

$$J_1 = \int_0^a \int_0^b \int_0^b {\mid f(x_1,x_2) - f(x_1,y_2) \mid^2}$$

$$( \int_0^a\frac{1} {({\mid x_1 -y_1 \mid + \mid x_2 - y_2 \mid})^{3}} dy_1) dy_2 dx_2 dx_1.$$

Lemma 2.3 with $y = \mid x_2 - y_2 \mid$, $t=y_1$, $x=x_1$, $c = a$ and $d=d$ implies

$$J_1 \le \int_0^a \int_0^b \int_0^b \frac{\mid f(x_1,x_2) - f... ...d x_2 - y_2 \mid^2}dy_2dx_2dx_1 = \mid f \mid^2_{H_a^{1/2}(Q)}$$

and thus the inequality $I_1 \le 2^{3/2}\mid f \mid^2_{H_a^{1/2}(Q)}$ is proved. The

$I_2 \le 2^{3/2}\mid f \mid^2_{H_b^{1/2}(Q)}$ inequality can be proved in a similar way and so the proof is completed.

Proof 2.9 (Proof of Theorem 2.1.)   It is easy to see that the inequalities of the Theorem 2.1 are simple combinations of the inequalities of Lemma 2.4 and Lemma 2.5.

Remark 2.10   The separability property in the $H^{1/2}(R^2)$ case is given in [3,8].

HEJ, HU ISSN 1418-7108 Manuscript no.: ANM-980205-A