HEJ, HU ISSN 1418-7108 Manuscript no.: ANM-980724-A

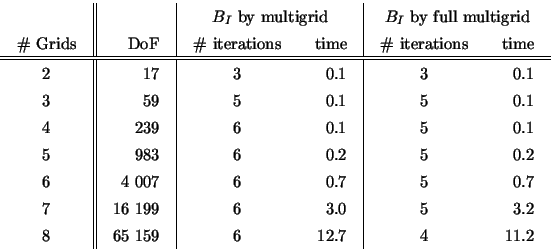
Model problem 1, criss-cross triangulation

Here we present a similar comparison as above and draw similar conclusions.

For a fixed $\omega \le 1.2$ full multigrid performs better (or not worse) than multigrid in terms of iteration numbers. Table 6 summarized the degrees of freedom and the computational time for $\omega = 1.0$.

The theoretical results of the full two-grid operator cannot be extended to this case since the whole analysis is based on the standard triangulation (which, in turn, implies a different stiffness matrix). The numerical results strengthen this point since the optimal smoothing parameter $\omega=1.0$ is smaller than with the standard triangulation.

A comparison of the iteration numbers for both types of the triangulation reveals its strong dependence on the coarse grid and on the smoothing parameter $\omega$.

 

Table: Model problem 1, criss-cross triangulation, # cg iterations

 

Table: Model problem 1, criss-cross triangulation, # cg iterations and time for $\omega=1.0$

HEJ, HU ISSN 1418-7108 Manuscript no.: ANM-980724-A