HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-980724-A
| 

 |
|
In the second column of Table 3 we consider the
special case of exact solvers (
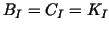 ). The bounded iteration
numbers confirm the spectral equivalence of ). The bounded iteration
numbers confirm the spectral equivalence of 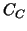 to to 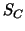 . .
In all other columns the three components 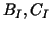 , and , and  are
chosen as described above.
The iteration numbers are compared for the MG and FMG
basis transformation, respectively, and for different smoothing
parameters are
chosen as described above.
The iteration numbers are compared for the MG and FMG
basis transformation, respectively, and for different smoothing
parameters 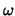 of of 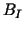 .
We observe that the cg iteration numbers depend heavily on
the proper choice of .
We observe that the cg iteration numbers depend heavily on
the proper choice of 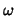 .
The best iteration numbers are obtained with .
The best iteration numbers are obtained with
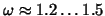 .
This corresponds to the theoretical results of the
full two-grid operator (cf. Figure 3).
Thus the theoretical results obtained there can be generalized (to some extent)
to the full multigrid operator. .
This corresponds to the theoretical results of the
full two-grid operator (cf. Figure 3).
Thus the theoretical results obtained there can be generalized (to some extent)
to the full multigrid operator.
For a fixed
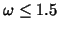 the comparison reveals that
FMG requires less (or no more) iterations than multigrid.
Finally, Table 4 summarized the degrees of freedom and the
computational time for the comparison reveals that
FMG requires less (or no more) iterations than multigrid.
Finally, Table 4 summarized the degrees of freedom and the
computational time for 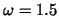 . .
Table:
Model problem 1, standard triangulation, # cg iterations
| |
Table:
Model problem 1, standard triangulation, # cg iterations and time for 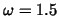
| |
| HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-980724-A
| 

 |
|