HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-980724-A
| 

 |
|
The Domain Decomposition Preconditioner
For the domain decomposition method (FE substructure technique) let
the domain 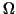 be subdivided into be subdivided into 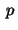 non-overlapping subdomains non-overlapping subdomains
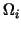 . The coupling boundary . The coupling boundary 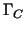 is defined as is defined as
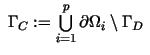 with with 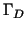 being the Dirichlet boundary.
The index `C' always refers to nodes on that coupling boundary being the Dirichlet boundary.
The index `C' always refers to nodes on that coupling boundary
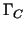 whereas the index `I' relates to nodes inside the subdomains whereas the index `I' relates to nodes inside the subdomains
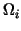 . Figure 1 may serve as an example. . Figure 1 may serve as an example.
For the finite element method used here we utilize the basis
 consisting of the common piecewise linear ansatz functions
consisting of the common piecewise linear ansatz functions 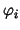 over the internal nodes of the
triangulation. Let the numbering be such that all ansatz functions
related to
over the internal nodes of the
triangulation. Let the numbering be such that all ansatz functions
related to 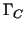 come first, followed by those related to
the inner nodes of come first, followed by those related to
the inner nodes of  , , 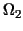 ...
With this special ordering the resulting system of linear equations
can be written in block form ...
With this special ordering the resulting system of linear equations
can be written in block form
The basis transformation of the FE basis  to
the approximate discrete harmonic basis to
the approximate discrete harmonic basis
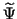 is given
by is given
by
The Additive Schwarz Method (ASM) corresponding to the splitting
of the finite element space into the subspaces
span
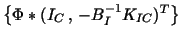 and
span and
span
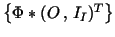 yields the preconditioner (cf. [12,13,23])
yields the preconditioner (cf. [12,13,23])
The matrices 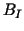 , ,
 , ,
 ,
and ,
and
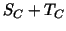 are referred to as
the basis transformation,
the Schur complement,
the perturbation of the Schur complement, and
the modified Schur complement, respectively.
are referred to as
the basis transformation,
the Schur complement,
the perturbation of the Schur complement, and
the modified Schur complement, respectively.
Finally the matrices 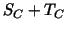 and and 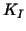 are replaced by symmetric,
positive definite and spectrally equivalent matrices are replaced by symmetric,
positive definite and spectrally equivalent matrices 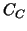 and and 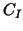 ,
i.e. ,
i.e.
It has been shown in [12,13] that the resulting preconditioner
![\begin{displaymath}
C := \left( \begin{array}[c]{cc}
{I_C} & {K_{CI}B_I^{-T}} ...
..._C} & {O} \\ {B_I^{-1}K_{IC}} & {I_I} \\
\end{array} \right)
\end{displaymath}](img64.gif) |
(1) |
is spectrally equivalent to 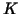 with the spectral condition number estimate with the spectral condition number estimate
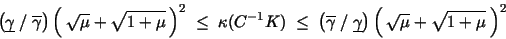 |
(2) |
Here
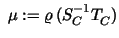 is the spectral radius
of is the spectral radius
of
 , and , and
 and
and
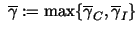 . .
In our examples the three components 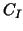 , , 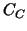 and and 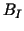 of
this preconditioner of
this preconditioner 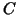 are chosen as follows: are chosen as follows:
These theoretical and numerical results indicate that the
spectral condition number
 depends heavily on
depends heavily on
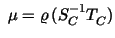 and thus on
and thus on
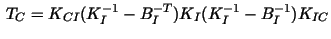 .
Hence the improvement of .
Hence the improvement of
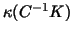 has to be achieved via
the basis transformation has to be achieved via
the basis transformation  . .
To our knowledge the use of the full multigrid technique for the
definition of the basis transformation  has not been investigated
theoretically.
The analysis of this method is a major aim of this paper. We try
to find out as to whether the has not been investigated
theoretically.
The analysis of this method is a major aim of this paper. We try
to find out as to whether the  -dependence of -dependence of
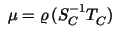 ,
as it occurs by applying only one multigrid step, can be overcome. ,
as it occurs by applying only one multigrid step, can be overcome.
| HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-980724-A
| 

 |
|