HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-980724-A

The model problems and the domains

Here we consider exclusively the Poisson equation with homogeneous Dirichlet boundary conditions:

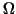$\begin{displaymath} \mbox{Find }\: u(x) \in H^1_o ( \Omega ) : \qquad \int_{\... ... = \, \int_{\Omega} f v \qquad \forall v \in H^1_o ( \Omega ) \end{displaymath}$

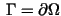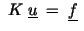and $\Omega$ being a bounded two-dimensional domain with Lipschitz-continuous boundary $\,\Gamma = \partial \Omega$ . By means of the usual linear triangular finite element discretization we obtain a system of linear equations $\; K \; \underline{u} \; = \; \underline{f} \;$ with a symmetric and positive definite matrix

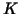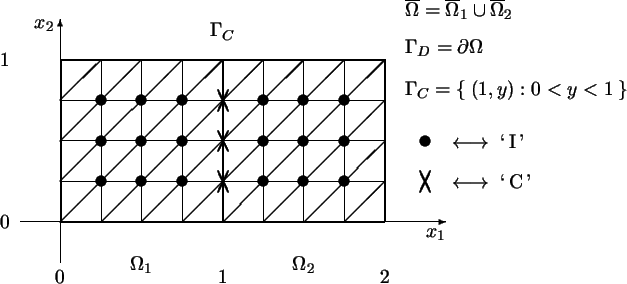
In this paper we consider two model problems. The model problem 1 is given by the differential equation mentioned above and the domain 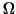$\Omega$ consisting of two unit squares. This domain is shown in Figure 1 which also illustrates some terms to be introduced later.

**Figure 1:** Model problem 1 (triangulation and subdomains)
$\begin{figure}\begin{center} \protect\begin{picture}(30,14) % \thinlines % \p... ... }} \end{picture} } \protect\end{picture} \\ \end{center}\protect\end{figure}$

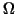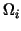The model problem analysis is performed exclusively on this model problem 1. For numerical experiments we also use the model problem 2. The corresponding domain $\Omega$ and the subdomains $\Omega_i$ are depicted in Figure 2.

**Figure 2:** Model problem 2
$\begin{figure}\begin{center} \protect\begin{picture}(8,5.5) % \thinlines % \... ...}} \end{picture} } \protect\end{picture} \\ \end{center} \protect\end{figure}$

For a further (real life) problem the reader is referred to [20].

HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-980724-A