Analysis of a special full two-grid operator
For the special case
where the smoothing parameter is chosen to be 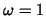 a proof
of the growth of a proof
of the growth of 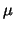 can be established. can be established.
Theorem 2
Consider the model problem 1 and the full two-grid operator
as 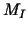 .
Suppose that bilinear interpolation and 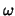 -Jacobi smoothing
with 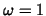 is used.
Then the behaviour of the spectral radius is
 as 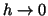 .
Proof:
For convenience we assume that 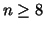 is a multiple of 4. is a multiple of 4.
Let the upper index (in parentheses) of a matrix or a vector
refer to the corresponding entry. With this notation we have
since ![$\, H_{[1]} \,$](img320.gif) is symmetric.
Additionally is symmetric.
Additionally
![$ \Lambda_{[k,1]} $](img321.gif) and thus and thus ![$ G_{[k,1]} $](img322.gif) (and (and ![$ H_{[1]} $](img323.gif) )
are positively semidefinit, and therefore )
are positively semidefinit, and therefore
![$\, G_{[k,1]}^{(1,1)} \ge 0 $](img324.gif) . .
We restrict  to values to values
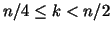 and
aim for a bound of and
aim for a bound of
![$\, G_{[k,1]}^{(1,1)} \,$](img327.gif) for such for such 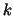 .
For simplicity we will omit the
index quadruplet .
For simplicity we will omit the
index quadruplet ![$[k,1]$](img329.gif) of the matrices of the matrices
![$G_{[k,1]} , \Lambda_{[k,1]} , \Theta_{[k,1]} $](img330.gif) , , ![$C_{[k,1]}$](img331.gif) and
and
![$\Gamma_{[k,1]}$](img332.gif) .
From (15) we obtain .
From (15) we obtain
with
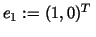 being the first unitary vector.
Utilizing the trigonometric identities we conclude being the first unitary vector.
Utilizing the trigonometric identities we conclude
with the new notation
This leads to
All entries of the diagonal matrix  are positive. This implies are positive. This implies
The first entry of  can be written as can be written as
with
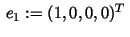 being the first unitary vector.
We will now investigate the vectors being the first unitary vector.
We will now investigate the vectors 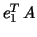 and and 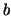 . .
Let us start with
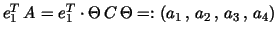 .
We perform one .
We perform one 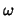 -Jacobi smoothing step with -Jacobi smoothing step with 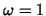 .
The corresponding matrix .
The corresponding matrix 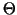 becomes becomes
In (9) the coarse grid correction matrix
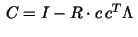 has been derived.
A cumbersome but straight-forward calculation results in has been derived.
A cumbersome but straight-forward calculation results in
Using
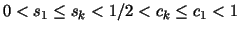 we obtain
the inequalities we obtain
the inequalities
Analogously the following bounds of the other entries
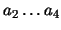 are derived: are derived:
The vector
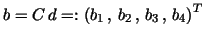 is dealt
with in a similar manner. From the expansion of is dealt
with in a similar manner. From the expansion of 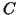 and and 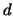 we
conclude we
conclude
As above, we similarly obtain
These estimates for 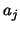 and and 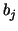 result in result in
Now the matrix entry
![$ H_{[1]}^{(1,1)} $](img365.gif) can be bounded
according to can be bounded
according to
Since
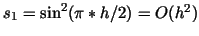 we conclude we conclude
Thus the desired spectral radius
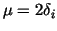 grows
(at least) like grows
(at least) like  as as  . .
|