The full two-grid operator
Let 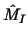 and and 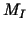 denote the two-grid operator and the full
two-grid operator, respectively. We will expand denote the two-grid operator and the full
two-grid operator, respectively. We will expand
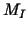 and then obtain an exact formula for and then obtain an exact formula for
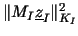 and eventually for and eventually for 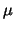 . .
We start by introducing the abbreviations
which yield obviously
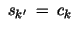 and and
 .
Let .
Let
![$[k,l] := \{ (k,l),(k',l),(k,l'),(k',l') \}$](img162.gif) be an index quadruplet.
Let be an index quadruplet.
Let
![$\;\underline{x}_{[k,l]} := [x_{k,l} , x_{k',l} , x_{k,l'} ,x_{k',l'} ]^T $](img163.gif) be that 4-dimensional subvector of a vector
be that 4-dimensional subvector of a vector
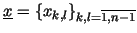 that corresponds to that corresponds to ![$[k,l]$](img165.gif) .
Analogously let .
Analogously let ![$X_{[k,l]}$](img166.gif) denote the denote the
 submatrix of a
(diagonal or block-diagonal) matrix submatrix of a
(diagonal or block-diagonal) matrix 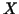 whose entries relate to whose entries relate to ![$[k,l]$](img169.gif) .
Let .
Let
![$[l] := \{l,l'\}$](img170.gif) be an index pair. Then be an index pair. Then ![$\sum_{[l]}$](img171.gif) and and
![$\sum_{[k,l]}$](img172.gif) shall denote the summation over all
index pairs and index quadruplets, respectively. shall denote the summation over all
index pairs and index quadruplets, respectively.
Let us now derive the expansion of 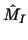 and and 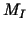 .
The two-grid operator .
The two-grid operator 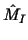 can be written as can be written as
The indices 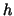 and and 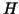 are related to the fine and coarse
grid, respectively.
We apply one are related to the fine and coarse
grid, respectively.
We apply one 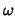 -Jacobi iteration for pre- and post-smoothing.
The following notation is used. -Jacobi iteration for pre- and post-smoothing.
The following notation is used.

The full two-grid technique means that the coarse grid system
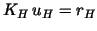 is solved first before taking the interpolant is solved first before taking the interpolant
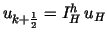 as the initial guess
of the subsequent two-grid iteration. Thus we have as the initial guess
of the subsequent two-grid iteration. Thus we have
(since we start with 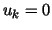 ). Therefore the error transition operator
of the full two-grid operator can be expressed as ). Therefore the error transition operator
of the full two-grid operator can be expressed as
This operator  will be expanded with respect to the orthonormal
basis will be expanded with respect to the orthonormal
basis
of the eigenvectors of  . Let the eigenvectors of an index quadruplet . Let the eigenvectors of an index quadruplet
![$[k,l]$](img189.gif) be placed in adjacent columns. The analysis of the appropriate
operators results in be placed in adjacent columns. The analysis of the appropriate
operators results in
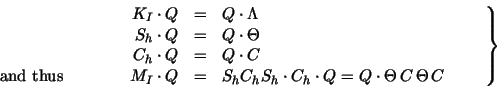 |
(8) |
The matrix  occurring in (8) has the form occurring in (8) has the form
The matrix 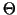 represents the represents the 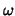 -Jacobi smoothing and thus
expands to -Jacobi smoothing and thus
expands to
The coarse grid correction matrix  has been derived in
[16] and [10] to be has been derived in
[16] and [10] to be
Here
![$\Lambda_{[k,l]}$](img212.gif) is the corresponding submatrix of is the corresponding submatrix of 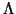 , i.e , i.e
Note that for 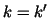 and/or and/or 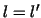 the matrix the matrix ![$C_{[k,l]}$](img217.gif) is reduced to the is reduced to the
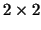 or or 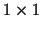 identity matrix.
Additionally the matrix identity matrix.
Additionally the matrix
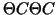 is block-diagonal and thus the
eigen subspace related to the quadruplet is block-diagonal and thus the
eigen subspace related to the quadruplet ![$[k,l]$](img221.gif) remains unchanged under the
application of the full two-grid operator remains unchanged under the
application of the full two-grid operator 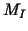 . .
Let us repeat the Fourier expansion (6) of
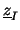 : :
Utilizing the matrix relations (8) we conclude
since 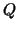 is an orthonormal basis. We introduce the new block-diagonal matrix is an orthonormal basis. We introduce the new block-diagonal matrix
and obtain the intermediate result
The substitution (12) of the 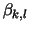 by the by the
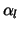 can be written as can be written as
and the definition
![$\underline{\alpha}_{[l]} := [\alpha_l , \alpha_{l'}]^T $](img250.gif) .
The application of this substitution results in .
The application of this substitution results in
with the new matrices
Thus the numerator of 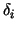 in (4) is evaluated. in (4) is evaluated.
The denominator of 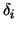 has been approximated in (5) as has been approximated in (5) as
Here ![$D_{[l]}$](img264.gif) and and 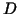 denote the positive definite diagonal matrices denote the positive definite diagonal matrices
Finally  can be expressed as can be expressed as
![\begin{displaymath}
\delta_i \; = \;
\sup\limits_{\underline{u}_C \in \rm R^{N...
...[l]} \; \varrho\left( D_{[l]}^{-1}
{H}_{[l]} \right) \qquad .
\end{displaymath}](img273.gif) |
(17) |
since 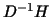 has a has a  block-diagonal form. block-diagonal form.
This last equation has been too difficult to analyse.
It allows, however, an exact numerical evaluation of 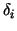 and thus of and thus of
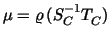 .
Table 1 comprises the the computed values of .
Table 1 comprises the the computed values of 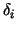 for decreasing
for decreasing 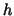 and for three smoothing parameters and for three smoothing parameters 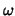 . .
Table:
Calculation of 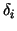 for the full two-grid operator for the full two-grid operator
|
|
Note that the maximum in (17) always occurs at
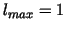 .
The results presented suggest the following .
The results presented suggest the following
Conjecture 1
Consider the model problem 1
(cf. Figure 1). Suppose the full two-grid operator with
bilinear interpolation and 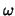 -Jacobi smoothing
is used as 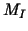 .
Then the spectral radius
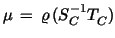
apparently grows like 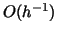 as 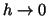 .
Remark 1
The growth of
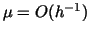 is obvious for 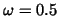 and
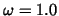 . In order to understand the different behaviour for
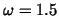 we have to look at equation ( 17).
The two diagonal entries of
![$ D_{[1]}^{-1} {H}_{[1]} $](img294.gif)
behave differently (in the numerical test). The right lower entry
(related to
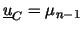 ) seems to be bounded and
dominates the spectral radius if 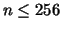 . The left upper entry
however (related to
 )
grows like 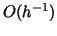 and takes over for  .
Remark 2
The dependence of 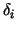 on the smoothing parameter 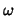 is
shown in Figure 3. Four different mesh sizes
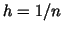 are considered.
Figure 3:
Dependence of 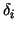 on on  for different for different 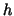
 |
Remark 3
For the multigrid method discussed here bilinear interpolation and the
transposed restriction is assumed. The common FEM interpolation is
not investigated since then (to our knowledge) no useful Fourier analysis of
the coarse grid correction matrix 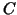 is possible.
|