HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-981030-A
| 

 |
|
In the recent years, growing computer resources have allowed
to perform three-dimensional electro-magnetic field calculations
[15,16,18].
One of the essential problems in 3D electromagnetics
is the necessity of gauging.
An additional gauging condition has to be imposed on the magnetic vector
potential to ensure its uniqueness. There are different gauging strategies
considered (see, e.g., [12,13,14]).
Sometimes, even an ungauged formulation (that may result in an indefinite
system of linear equations) is solved by iterative methods [11].
Another strategy uses a well-defined iteration process to approximate
the solution of an ungauged formulation [17].
>From the mathematical point of view, we have to
choose appropriate spaces.
In [9], the first author proposed a mixed variational formulation
in
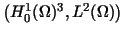 .
Indeed, existence and uniqueness results as well as discretization error estimates for classes of simple nodal elements
(e.g. the Mini element) have been proved.
Unfortunately, the mixed variational formulation does not correspond completely
with the magnetostatic problem.
Moreover, it has been stated in [5] that
magnetic field problems should rather be formulated
in .
Indeed, existence and uniqueness results as well as discretization error estimates for classes of simple nodal elements
(e.g. the Mini element) have been proved.
Unfortunately, the mixed variational formulation does not correspond completely
with the magnetostatic problem.
Moreover, it has been stated in [5] that
magnetic field problems should rather be formulated
in
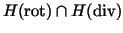 instead of
instead of 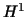 .
Therefore, the aim of the present paper is to establish
a mixed variational formulation
for linear and nonlinear magnetostatic problems
in the space .
Therefore, the aim of the present paper is to establish
a mixed variational formulation
for linear and nonlinear magnetostatic problems
in the space
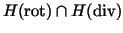 .
Here, we formulate the flux-surface boundary condition as a Dirichlet condition
with respect to the tangential components of the vector potential only,
and a Neumann condition with respect to its normal component.
The Dirichlet condition has been proposed, e.g., in [2], whereas
the Neumann condition was not explicitly stated therein, but implicitly
contained in the formulation.
Thus, we set up the problem in the space .
Here, we formulate the flux-surface boundary condition as a Dirichlet condition
with respect to the tangential components of the vector potential only,
and a Neumann condition with respect to its normal component.
The Dirichlet condition has been proposed, e.g., in [2], whereas
the Neumann condition was not explicitly stated therein, but implicitly
contained in the formulation.
Thus, we set up the problem in the space
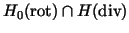 .
Other boundary conditions can be formulated in a similar manner.
As in the 2D case, cf. [8], additional assumptions with respect to
the coefficient allow a rigorous analysis of nonlinear problems. In particular, the
coefficient depends on the solution itself. Assumptions which are physically meaningful
and that guarantee unique solveability are stated.
The rest of the paper is organized as follows.
In Section 2, we discuss the physical model.
We present the variational formulation for linear magnetostatic
problems in Section 3
and give analytical results.
Section 4 is devoted to the results for nonlinear
magnetostatic problems.
Finally, we add some concluding remarks in Section 5. .
Other boundary conditions can be formulated in a similar manner.
As in the 2D case, cf. [8], additional assumptions with respect to
the coefficient allow a rigorous analysis of nonlinear problems. In particular, the
coefficient depends on the solution itself. Assumptions which are physically meaningful
and that guarantee unique solveability are stated.
The rest of the paper is organized as follows.
In Section 2, we discuss the physical model.
We present the variational formulation for linear magnetostatic
problems in Section 3
and give analytical results.
Section 4 is devoted to the results for nonlinear
magnetostatic problems.
Finally, we add some concluding remarks in Section 5.
| HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-981030-A
| 

 |
|