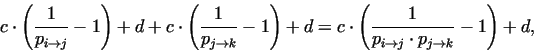HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-991102-A
| 

 |
|
To avoid the dangerous situations we have to know in every condition, how
close the system will be to the danger after the next step. In real life
usually we know only the probability of a transition between conditions,
the distance is unknown. Thus, it is useful to find a connection
between the two models, and for us now it is more important the transition,
which makes distance from probability.
So we are looking for a function
![$\mu: (0,1] \rightarrow \mathbf{R}_0^+$](img47.gif) , which has the following properties: , which has the following properties:
- (i)
- continuous,
- (ii)
- strictly monotonously decreasing,
- (iii)
-
- (iv)
-
- (v)
- for paralell ways we have
where 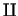 is a paralell composition operator. is a paralell composition operator.
Considering properties (i)-(iii) we have more different function-candidates,
e.g.
However, from property (iv), which can be rewritten in the form
follows, that the solution can only be some kind of logarithmic function ([3]).
EXAMPLE
Let us investigate the problem with the candidate
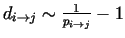 .
In this case we search the solution in the form .
In this case we search the solution in the form
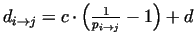 .
From property (iv) the following equality holds: .
From property (iv) the following equality holds:
from which with simple transformations
Thus, we are not able to choose 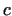 and and 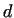 independently from independently from
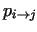 and and
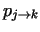 , so this function is not
appropriate. , so this function is not
appropriate.
So for our function
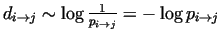 .
Knowing that .
Knowing that
 , we have , we have
 .
Obviously .
Obviously
and assuming the form
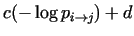 we can choose we can choose
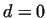 . The base of the logarithm can be an arbitrary number . The base of the logarithm can be an arbitrary number  , with , with
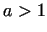 from property (ii).
Thus, we have the desired connection between the two models. We can specify
the distance from the danger (starting from the probability model) in the
following manner: from property (ii).
Thus, we have the desired connection between the two models. We can specify
the distance from the danger (starting from the probability model) in the
following manner:
- a)
- Starting from a given condition we specify the probability of reaching the
danger(ous conditions).
- b)
- Using the logarithmics proportionality we change to the distance model,
getting so the distance from the danger (finally, we apply a constant
multiplier if needed).
EXAMPLE
Let us assume, that in a whole-type probability model from a given condition
 we can go directly into three conditions, from which two are
dangerous ( we can go directly into three conditions, from which two are
dangerous (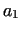 and and 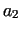 ). How far are we from the danger? ). How far are we from the danger?
System:
where
 , ,
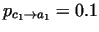 , ,
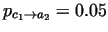 .
Then .
Then
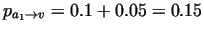 , ,
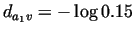 .
Applying a probability estimate .
Applying a probability estimate
i.e. the system
runs into danger in  steps, prospectively.
Since steps, prospectively.
Since
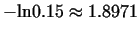 , using the function ln it is
suitable to apply a constant multiplier , using the function ln it is
suitable to apply a constant multiplier 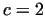 to get the correct distance. to get the correct distance.
Let us denote the inverse of function
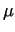 with with
![$\pi:\mathbf{R}_0^+ \rightarrow [0,1]$](img80.gif) .
Then .
Then 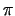 assures way through from distance model to probability model.
Its required properties can be written similarly, as those of function assures way through from distance model to probability model.
Its required properties can be written similarly, as those of function
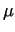 : :
- (i)
- continuous,
- (ii)
- strictly monotonously decreasing,
- (iii)
-
- (iv)
-
- (v)
- for paralell ways we have
Similarly as above it can be proved, that 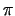 is some kind of
exponential function. Usually it can be written in the form is some kind of
exponential function. Usually it can be written in the form
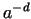 , where , where 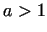 from property (ii). from property (ii).
| HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-991102-A
| 

 |
|