HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-991102-A
| 

 |
|
From property (iv) of functions 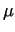 and and 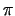 we have to specify operator
we have to specify operator 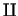 so,
that it has to satisfy the following two equalities: so,
that it has to satisfy the following two equalities:
Above we have applied the
harmonic average to "produce" operator 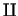 , but
- as it will be presented below - we are not able
to fit it exactly to these requirements.
From the definitions of functions , but
- as it will be presented below - we are not able
to fit it exactly to these requirements.
From the definitions of functions 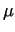 and and 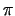 follows follows
so we would need
Choosing
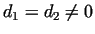 we get we get
with the obligation, that this must be held for all 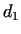 .
This is clearly not possible.
Thus, we have ``two different'' operators .
This is clearly not possible.
Thus, we have ``two different'' operators 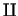 .
Using the harmonic average we get only an approach.
The result is exact if one of the distances .
Using the harmonic average we get only an approach.
The result is exact if one of the distances 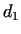 and and 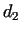 is
is 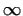 , in other cases there is an error-term.
However, this approach is well useable, because of its simplicity.
But, by an exact transition from probability model to distance model,
we have to use the logarithmic formula for operator , in other cases there is an error-term.
However, this approach is well useable, because of its simplicity.
But, by an exact transition from probability model to distance model,
we have to use the logarithmic formula for operator 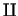 . .
| HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-991102-A
| 

 |
|