HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-000926-A |  
![[*]](http://heja.szif.hu/Icons/vissza1.gif)
![[*]](http://heja.szif.hu/Icons/elore1.gif) |
|
Given a number 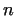 , it is a very important question,
how to construct its complete factorization according to Theorem 2.
Up to the , it is a very important question,
how to construct its complete factorization according to Theorem 2.
Up to the 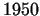 s, this process was usually very circumstantial
- and in most of the cases unsuccessful - for large numbers.
In spite of this a number of very important
theoretical results were published already long before
(e.g. by FERMAT).
However, the significant development in this field practically
started with the appearance of computers.
Similarly as before, we present only the most important
results and only some of the proofs. We omit the exact behaviour-analysis by
the methods.
Detailed theoretical discussion can be
found e.g. in [1]. s, this process was usually very circumstantial
- and in most of the cases unsuccessful - for large numbers.
In spite of this a number of very important
theoretical results were published already long before
(e.g. by FERMAT).
However, the significant development in this field practically
started with the appearance of computers.
Similarly as before, we present only the most important
results and only some of the proofs. We omit the exact behaviour-analysis by
the methods.
Detailed theoretical discussion can be
found e.g. in [1].
The basic algorithm
A traditional method for the factorization is the trial divison with the
primes
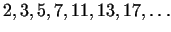 , or with the numbers , or with the numbers
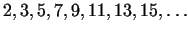 , which is easier to programize, but we get
the result slower. Analysing this algorithm (e.g. its simplified Maple-form
below) we conclude, that it works usable in our PC's if the order of , which is easier to programize, but we get
the result slower. Analysing this algorithm (e.g. its simplified Maple-form
below) we conclude, that it works usable in our PC's if the order of
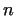 is maximum is maximum
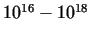 , or if the order of the divisor is maximum , or if the order of the divisor is maximum
 . For larger numbers the algorithm usually
slows down hopelessly, because of the lot of divisions. In a faster computer
we can make this situation better, but the improvement will not be
spectacular.
In the following example we search for the prime divisors of an odd number with
trial divison. We can get the same result using the . For larger numbers the algorithm usually
slows down hopelessly, because of the lot of divisions. In a faster computer
we can make this situation better, but the improvement will not be
spectacular.
In the following example we search for the prime divisors of an odd number with
trial divison. We can get the same result using the ifactor
function with the option 'easy'.
> basic:=proc(n,limit)
> local i,s,a;
> s:=NULL; a:=n;
> for i from 3 by 2 to limit do
> if a mod i = 0 then a:=a/i; s:=s,i;
> while a mod i = 0 do a:=a/i; s:=s,i od
> fi
> od; print(s,a)
> end:
> b:=1234567890123456789:
> basic(b, 4001);
> ifactor(b,'easy');
Let us assume, that the number 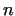 is very large, it contains e.g. is very large, it contains e.g. 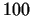 decimal digits. In this case we apply the
basic algorithm to separate the "small" factors up to the order of
approximately
decimal digits. In this case we apply the
basic algorithm to separate the "small" factors up to the order of
approximately  . After this we examine the remaining part further with
additional methods, discussed in the following subsections. . After this we examine the remaining part further with
additional methods, discussed in the following subsections.
Subsections
| HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-000926-A |  
![[*]](http://heja.szif.hu/Icons/vissza1.gif)
![[*]](http://heja.szif.hu/Icons/elore1.gif) |
|