HEJ, HU ISSN 1418-7108 Manuscript no.: ANM-000926-A

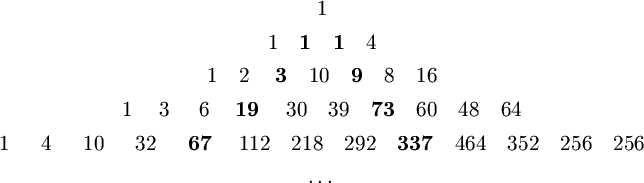
Application in generalized Pascal's triangles

In this section we apply the methods discussed in the previous subsection to prove exactly the prime property of a large number in a generalized Pascal's triangle. The theory of these triangles was presented by the author in 1997 ([7]). The general triangles were specified as follows:
DEFINITION. (generalized Pascal's triangle) Let $0\le a_0,a_1,a_2\dots a_{m-2},a_{m-1}\le 9$ be integers. Then we can get the $k$th element in the $n$th row of the $a_0a_1a_2\dots a_{m-2}a_{m-1}$-based triangle if we multiply the $(k-m)$th element in the $(n-1)$th row by $a_{m-1}$, the $(k-m+1)$th element in the $(n-1)$th row by $a_{m-2}$, $\dots$, the $(k-1)$th element in the $(n-1)$th row by $a_1$, the $k$th element in the $(n-1)$th row by $a_0$, and add the products. If for some $i$ we have $k-m+i< 0$ or $k-m+i> n-1$ (i.e. some element in the $(n-1)$th row does not exist according to the traditional implementation) then we consider this element to be 0. The indices in the rows and columns of the triangle run from 0.
In [7] the most important properties of these triangles were thoroughly investigated. Among others we gave a direct formula for the $k$th element in the $n$th row, thus we are able to specify an element somewhere in a generalized triangle without building the preceding rows. Investigating the elements in these triangles we can find a number of large primes. It is a conjecture, that we are able to find $\textit{arbitrary}$ large primes too, so with the building of the triangles we get some kind of "prime formula". For example in the first 150 rows in the $1114$ based triangle with a Maple program using the isprime function we found the elements in the following (row, column) position to be prime:

$$(2,2), (3,3), (3,6), (4,4), (4,8), (5,5), (10,10), (23,46), (31,62),$$

$$(48,48), (116,116), (132,132), (144,144).$$

Here the last element contains 93 decimal digits. In Figure 1 we present the first few row of this triangle.

  

Figure 1: The 1114-based triangle

Analysing the structure of the $abcd$ based triangle, we conclude, that prime elements can only take place in the positions $(n,n)$ and $(n,2n)$ - this follows from Theorem 2 in [7]. The elements in these positions are presented with bold characters. We mentioned above, if the isprime function says, that a number is prime, it is not surely true. Thus if we would like to make sure about this property, we have to use the methods discussed in the previous subsection.

Exact proof for a prime candidate In the following part we prove exactly the prime property of the element in the position $(116, 116)$, which is

  > a:=113339208484022902352005233461239034435177252913302015
  > 128561961100032061289;

a number containing $75$ digits. Testing this number with the isprime function we get

  > isprime(a);

$${\it true}$$

thus $a$ is very likely prime. To prove this, we need the factorization of $a-1$. We use first the easy option, because else we can run in a very long unsuccessful cycle.

  > ifactor(a-1,'easy');

$$(\,{\rm }2)^{3}\,(\,{\rm }3)\,{\it\_c69}\,(\,{\rm }5399)$$

  > b:=(a-1)/(2^3*3*5399);

$$b := 874692909829157423843962103022465845798429129725427665065768 \backslash$$

$$051954313 \hspace{5cm}$$

  > isprime(b);

$${\it false}$$

Knowing that $b$ is not prime, we have a $69$-digit number to factorize. It is usually hopeless in a PC, but now we are lucky, with the pollard option we can break this number in approximately $15$ minutes ³. Without this option, with the basically interpreted Morrison-Brillhart method, the ifactor will stay unsuccesful for much longer time.

  > ifactor(b,'pollard');

$$(\,{\rm } 10819096345425007095734545669640557980594988462603498411463)$$

$$(\,{\rm }80847131951)\mbox{\hspace{188pt}}$$

  > c:=b/80847131951:

Observing, that the Maple-system writes the complete factorization only if the factors are prime (in the other case e.g. for $c$ we would have _c59), we know, that investigating $c$ with the ifactor function we get the answer true. However, we have to prove this too. The question arises, when can we believe "surely" the Maple-system if it says, that a number is prime. Analysing the operation of the isprime function with the following commands ⁴

  > interface(verboseproc=2):
  > print(isprime);

we conclude, that the system examines gcd-s up to approximately $10^6$, so very strictly this is the lower bound. However, the Maple guarantees the safety for much larger numbers, too. In this paper we fix our lower bound - considering the point of view of safety and decreasing the use up of space - at 20 decimal digits. Thus we believe the true answer of the isprime function without reservation up to this bound (it is an easy exercise to check, that the prime numbers below this bound are really primes). Turning back to the number $c$, we have to factorize $c-1$.

  > ifactor(c-1,'easy');

$$(\,{\rm }2)\,(\,{\rm }23)\,(\,{\rm }617)\,(\,{\rm } 381195699578077904859930437236296172947466297745172941)$$

  > d:=(c-1)/(2*23*617):

Now we have a $54$ digit large prime candidate, let us continue with $d-1$.

  > ifactor(d-1,'easy');

$$(\,{\rm }2)^{2}\,(\,{\rm }5)\,(\,{\rm }7)^{2}\,(\,{\rm }11)... ...\,{\rm }853)\,{\it\_c35}\,(\,{\rm } 551231)\,(\,{\rm }17977)$$

  > e:=(d-1)/(4*5*49*11*13*29*853*17977*551231);

$$e := 11096550617640991328150412126833359$$

We know surely, that this $35$ digit number is not prime. The Maple is able to factorize it in $15$ minutes.

  > ifactor(e);

$$(\,{\rm }51386119357470140587)\,(\,{\rm }215944514907757)$$

So finally we have a complete factorization, thus we begin the exact proofs. First we prove the prime property of $d$ with the method of POCKLINGTON.

  > f:=215944514907757:
  > g:=51386119357470140587:
  > modp(power(2,d-1),d);

$$1$$

Observing, that $f \cdot g > [\sqrt{d}]$ we have to check only two gcd-s.

  > gcd(modp(power(2,(d-1)/f),d),d);

$$1$$

  > gcd(modp(power(2,(d-1)/g),d),d);

$$1$$

Thus $d$ is prime, we can continue with $c$. Now we use the method of BRILLHART, LEHMER and SELFRIDGE, because $c-1$ has only a few prime divisors.

  > modp(power(2,(c-1)/d),c);

$$5070659633100738759368526184715994149200912905277760631436$$

Similarly we get very large results for modp(power(2,(c-1)/617),c) and modp(power(2,(c-1)/23),c). Here we disregarded the details. With our last exponent first we are unsuccessful.

  > modp(power(2,(c-1)/2),c);

$$1$$

Choosing another base we get

  > modp(power(3,(c-1)/d),c);

$$3577790411510843518520960690125390427481232559654805086366$$

thus we are ready with $c$. To the prime property of $a$, we observe, that $c$ is much larger, than the product of the other factors of $a-1$, i.e. with the POCKLINGTON method we need to compute only one gcd.

  > modp(power(2,a-1),a);

$$1$$

  > gcd(modp(power(2,(a-1)/c),a),a);

$$1$$

With this we have proved exactly the prime property of $a$.

Conclusions Summarizing, we have found very large primes in the generalized Pascal's triangles, and the Maple system was able to prove exactly the prime property of one candidate.

HEJ, HU ISSN 1418-7108 Manuscript no.: ANM-000926-A