|
Basic propertiesThe proofs can be found in any textbook on calculus.
EXAMPLE 2.2.
(c) shows that in EXAMPLE 1.4 the function
is integrable, whereas (h) implies that int_step( 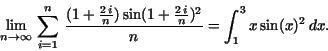
Exercise 2.1.
Prove that
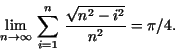
Hint: Look at
|
|
|
Basic propertiesThe proofs can be found in any textbook on calculus.
EXAMPLE 2.2.
(c) shows that in EXAMPLE 1.4 the function
is integrable, whereas (h) implies that int_step( 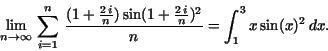
Exercise 2.1.
Prove that
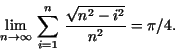
Hint: Look at
|
|