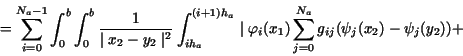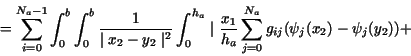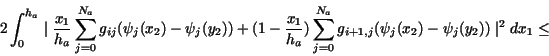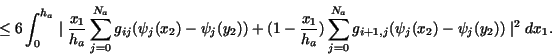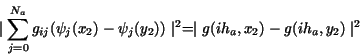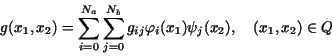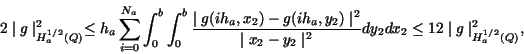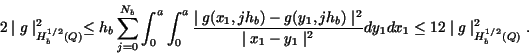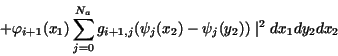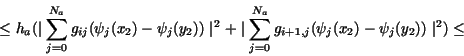|
Let us assume that the intervals ![$[0,a]$](img66.gif) and and ![$[0,b]$](img67.gif) are endowed with
equidistant meshes corresponding to the grid sizes are endowed with
equidistant meshes corresponding to the grid sizes 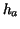 and and 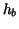 ,
respectively and let ,
respectively and let
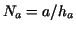 and and 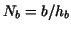 .
We discretize .
We discretize
![$Q = [0,a] \times [0,b]$](img72.gif) as a direct product of the
discretizations defined on the intervals as a direct product of the
discretizations defined on the intervals ![$[0,a]$](img66.gif) and and ![$[0,b]$](img67.gif) .
The elements of the piecewise bilinear finite element space .
The elements of the piecewise bilinear finite element space 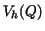 corresponding to this discretization can be expressed as
corresponding to this discretization can be expressed as
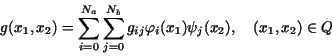 |
(14) |
where 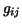 denote the function values at the grid points denote the function values at the grid points 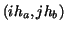 and
and 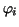 and and 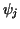 are the one-dimensional piecewise linear
shape funcions corresponding to the discretization of the intervals are the one-dimensional piecewise linear
shape funcions corresponding to the discretization of the intervals ![$[0,a]$](img66.gif) , ,
![$[0,b]$](img67.gif) , respectively. , respectively.
In this space the 'partial' seminorms
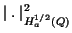 and and
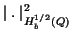 can be simplified to a sum of one-dimensinal seminorms:
can be simplified to a sum of one-dimensinal seminorms:
Theorem 3.1
Let 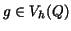 . Then
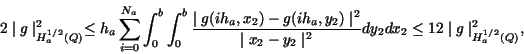 |
(15) |
and
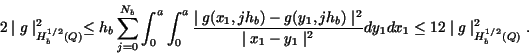 |
(16) |
The proof of the theorem is based on the following lemma.
Lemma 3.2
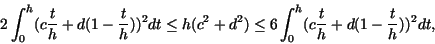 |
(17) |
Proof 3.3
Since
the inequality
proves our lemma.
Proof 3.4 (Proof of Theorem 3.1.)
In the case of 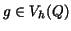 for the seminorm

the following indentities hold:
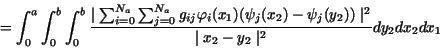 |
(18) |
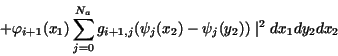 |
(19) |
 |
(20) |
Using Lemma 3.2 with  , , 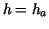 , ,
 and and
 one can get
one can get
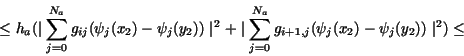 |
(21) |
Consider
and summing up (21) for 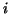 , (20) implies the inequality (15).
The inequality (16) can be proved analogously. , (20) implies the inequality (15).
The inequality (16) can be proved analogously.
|