HEJ, HU ISSN 1418-7108 Manuscript no.: ANM-981030-A

Interface conditions

Let us assume that there are different material coefficients (e.g., for iron and air) in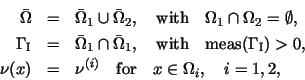 $\Omega$, i.e., without loss of generality we have an interface $\Gamma_{\rm I}$ and

$$\begin{eqnarray*} \bar\Omega &=& \bar\Omega_1 \cup \bar\Omega_2,\quad{\rm with}... ...&=& \nu^{(i)} \quad{\rm for}\quad x \in \Omega_i,\quad i=1, 2, \end{eqnarray*}$$

and we find (classical) solutions of (6), ${\vec{\rm {A}}}^1$ in $\Omega_1$ and ${\vec{\rm {A}}}^2$ in $\Omega_2$. The physical interface conditions are well known, it is observed that the normal component of ${\vec{\rm {B}}}$ and the tangential component of ${\vec{\rm {H}}}$ are continuous. We will demonstrate that these conditions are quite naturally included in a variational formulation using a continuous vector potential ${\vec{\rm {A}}}$. On one hand,

$${\vec{\rm {A}}}_{\rm t}^1 = {\vec{\rm {A}}}_{\rm t}^2 \quad{\rm on}\quad \Gamma_{\rm I}$$

implies the ''strong'' first interface condition

$${\vec{\rm {B}}}_{\rm n}^1 = {\vec{\rm {B}}}_{\rm n}^2 \quad{\rm on}\quad \Gamma_{\rm I}.$$

On the other hand, it follows from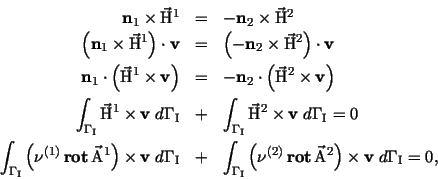

$${\vec{\rm {H}}}_{\rm t}^1 = {\vec{\rm {H}}}_{\rm t}^2 \quad{\rm on}\quad \Gamma_{\rm I}$$

that

$$\begin{eqnarray*} {\bf n}_1 \times {\vec{\rm {H}}}^1 &=& -{\bf n}_2 \times {\ve... ...{\rm {A}}}^2 \right) \times {\bf v} \;d{\Gamma_{\rm I}} = 0, \end{eqnarray*}$$

and the line integrals over the interface will cancel out, i.e., the second interface condition is contained in a ''weak'' sense in the variational formulation. Thus, the variational formulation presented in the following is the correct representation of the physical behaviour. We remark that the variational formulation can be derived from the energy functional of the magnetic field,

$$W = \frac{1}{2} \int_\Omega {\vec{\rm {B}}} \cdot {\vec{\rm {H}}} \;dx$$

too, and that the second interface condition is not included so naturally if a $-\Delta{\vec{\rm {A}}} = {\vec{\rm {J}}}$ formulation is used.

HEJ, HU ISSN 1418-7108 Manuscript no.: ANM-981030-A