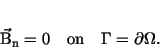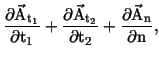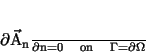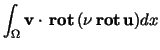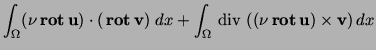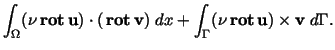HEJ, HU ISSN 1418-7108 Manuscript no.: ANM-981030-A

Boundary conditions

The physical model would lead us to a problem in an infinite domain with Sommerfeld's radiation condition, cf. [10]. However, in many practical cases we may assume that the field lines of the magnetic induction ${\vec{\rm {B}}}$ do not enter or leave a bounded domain $\Omega\subset{\bf R}^3$ representing the device (e.g. the machine). The latter condition, called flux-surface condition, requires that the normal component vanishes on the boundary $\Gamma=\partial\Omega$ which is assumed to be sufficiently smooth, i.e.

$${\vec{\rm {B}}}_{\rm n} = 0 \quad {\rm on} \quad \Gamma = \partial\Omega.$$ (11)

Suppose for the moment that the normal direction is in the z direction of the Cartesian coordinate system. Then we have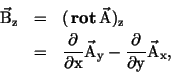

$$\begin{eqnarray*} {\vec{\rm {B}}}_{\rm z} &=& ({ \bf rot }{\vec{\rm {A}}})_{\... ...y} - \frac{\partial}{\partial \rm y} {\vec{\rm {A}}}_{\rm x}, \end{eqnarray*}$$

and ${\vec{\rm {B}}}_{\rm z} = 0$ is an immediate consequence of

$${\vec{\rm {A}}}_{\rm x} = {\vec{\rm {A}}}_{\rm y} = { \rm const }= 0.$$

Therefore, we will demand that the tangential components of ${\vec{\rm {A}}}$ vanish on $\Gamma$, i.e.

 

$${\vec{\rm {A}}}_{\rm t} = {\bf0} \quad {\rm on} \quad \Gamma = \partial\Omega,$$ (12)

$${\vec{\rm {A}}} \times {\bf n} = {\bf0} \quad {\rm on} \quad \Gamma = \partial\Omega.$$

If (12) holds on a smooth surface, then we get

$$\div {\vec{\rm {A}}} = \frac{\partial{\vec{\rm {A}}}_{\rm t_1}}{\partial{\rm t}_1} + \fr... ...}{\partial{\rm t}_2} + \frac{\partial{\vec{\rm {A}}}_{\rm n}}{\partial{\rm n}},$$

$$\div {\vec{\rm {A}}} = \frac{\partial{\vec{\rm {A}}}_{\rm n}}{\partial{\rm n}},$$ (13)

if ${\rm t_1}$ and ${\rm t_2}$ denote two perpendicular tangential unit vectors. Thus, in view of (5), we should formulate a Neumann condition

$$\frac{\partial{\vec{\rm {A}}}_{\rm n}}{\partial{\rm n}} = 0 \quad {\rm on} \quad \Gamma = \partial\Omega$$ (14)

for the normal component rather than a Dirichlet condition. Before we discuss the interface conditions, we perform the standard procedure for getting a variational formulation from (8), i.e. we multiply with a test function v and obtain

 

$$\check{a}({\bf u},{\bf v}) = \int_{\Omega} {\bf v} \cdot { \bf rot }(\nu { \bf rot }{\bf u}) dx$$

$$= \int_{\Omega} (\nu { \bf rot }{\bf u}) \cdot ({ \bf rot }{\bf... ...+ \int_{\Omega} \div\left( (\nu { \bf rot }{\bf u}) \times {\bf v} \right) dx$$

$$= \int_{\Omega} (\nu { \bf rot }{\bf u}) \cdot ({ \bf rot }{\bf v}) \;dx + \int_{\Gamma} (\nu { \bf rot }{\bf u}) \times {\bf v} \; d\Gamma.$$ (15)

The second integral will be zero if ${\bf v}\times{\bf n}\vert _{\Gamma}=0$, i.e. ${\bf v}_{\rm t}\vert _{\Gamma} = 0$. The latter will be satisfied if ${\bf v}$ is taken from an appropriate test space related to ${\bf u}$, see Subsection 3.1.

HEJ, HU ISSN 1418-7108 Manuscript no.: ANM-981030-A