HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-980724-A
| 

 |
|
The interest in parallel solvers for partial differential equations has
risen in recent years.
Thus the domain decomposition method (DD) became increasingly popular
since it contains a natural parallel structure.
As it is usual with this method, we utilize the resulting block system
of linear equations
(cf. section 3 for a more detailed description).
The Additive Schwarz Method has been employed to construct preconditioners 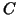 of the type
of the type
for the (parallel) conjugate gradient method
(cf. [12,13], and section 3).
Two of the three components of this
DD preconditioner, namely the (modified) Schur complement preconditioner 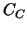 ,
and the local Dirichlet problem preconditioner ,
and the local Dirichlet problem preconditioner 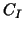 , have been studied
intensively by the DD community
(cf. the proceedings of the international Symposia on ``DD methods for partial differential equations'' since 1987
[7,3,4,8,,1,19], and also [2,5,6]).
Haase/Langer/Meyer [12,13] proved that the quality
of the DD preconditioner is dominantly influenced by the third component,
the basis transformation , have been studied
intensively by the DD community
(cf. the proceedings of the international Symposia on ``DD methods for partial differential equations'' since 1987
[7,3,4,8,,1,19], and also [2,5,6]).
Haase/Langer/Meyer [12,13] proved that the quality
of the DD preconditioner is dominantly influenced by the third component,
the basis transformation  .
This basis transformation determines the perturbation .
This basis transformation determines the perturbation 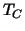 of the Schur
complement which, in turn, influences the spectral radius of the Schur
complement which, in turn, influences the spectral radius
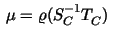 and finally the relative condition number of the preconditioner,
and finally the relative condition number of the preconditioner,
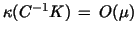 (provided that (provided that  and and 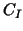 are
chosen appropriately). are
chosen appropriately).
Several ideas to choose the basis transformation 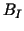 which is defined
implicitly by some iteration method are summarized
in section 3. Our interest is focused on the multigrid
method for which it is known that which is defined
implicitly by some iteration method are summarized
in section 3. Our interest is focused on the multigrid
method for which it is known that
In this paper we investigate the use of one full multigrid cycle
for the definition of the basis transformation. Special interest is paid
firstly as to whether the increasing condition number
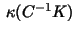 can be overcome as
can be overcome as 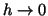 , and secondly to the computational expense. , and secondly to the computational expense.
Sections 2 is devoted to the model problems
whereas section 3 deals with the DD preconditioner
and the basis transformation 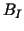 .
The theoretical analysis of the full multigrid basis transformation
is performed in section 4.
Unfortunately the analysis turned out to be so technical that only the
full two-grid operator on a simple model problem could be treated.
In section 5 the numerical experiments with the
full multigrid operator are given. Section 6
summarizes the results obtained. .
The theoretical analysis of the full multigrid basis transformation
is performed in section 4.
Unfortunately the analysis turned out to be so technical that only the
full two-grid operator on a simple model problem could be treated.
In section 5 the numerical experiments with the
full multigrid operator are given. Section 6
summarizes the results obtained.
| HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-980724-A
| 

 |
|
![\begin{displaymath}
\left( \begin{array}[c]{cc}
{ K_C } & { K_{CI} } \\
{ K_...
...}
{\underline{f}_C} \\ {\underline{f}_I}
\end{array} \right)
\end{displaymath}](img5.gif)