The domain decomposition (DD) technique is well-suited for constructing
parallel partial differential equation solvers.
By means of the Additive Schwarz Method we derive and analyse Dirichlet-type DD preconditioners.
Such preconditioners contain three components which are the
(modified) Schur complement preconditioner, the local Dirichlet problem
preconditioner, and the so-called basis transformation.
Of all components, the last one plays the most crucial role.
Amongst other methods, multigrid techniques have been popular for defining
this basis transformation. However, the quality of the preconditioner
deteriorates as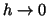 
.
In this paper we investigate whether the use of the full multigrid method
can remedy this shortcoming.
The technical theoretical analysis has been carried out for a model problem and
the full two-grid operator.
In numerical experiments the full multigrid basis transformation
has been tested.
The analysis shows that full multigrid behaves asymptotically as
the multigrid method but displays better numerical performance.
