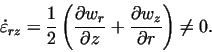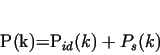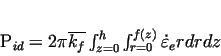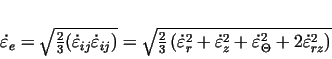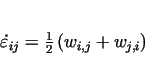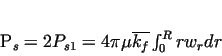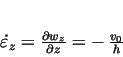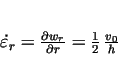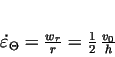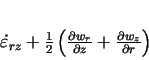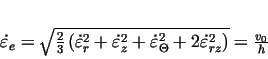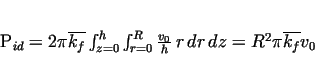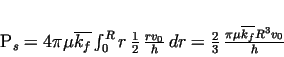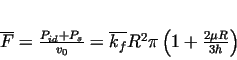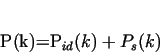Submitted to HEJ
Manuscript no.: MET-990617-A |  

 |
|
The power requirement of forming is composed as a sum of two components:
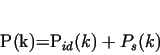 |
(15) |
where 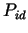 is the pure power requirement of forming, while is the pure power requirement of forming, while 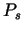 is the
friction power which arises between the contact surfaces of the piece and the
pressure plates.
Calculation of components see [3] for details: is the
friction power which arises between the contact surfaces of the piece and the
pressure plates.
Calculation of components see [3] for details:
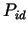 is the power of pure deformation: is the power of pure deformation:
where  is the forming strength of the material and is the forming strength of the material and
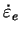 is the comparative deformation velocity. is the comparative deformation velocity.
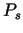 is the friction power: is the friction power:
assuming the
 which is the Coulomb friction.
The which is the Coulomb friction.
The 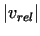 is the relative
displacement of the piece and the die at the contacting surfaces. is the relative
displacement of the piece and the die at the contacting surfaces.
In details, with considering deformation strength at the mean value:
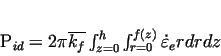 |
(16) |
where
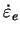 comparative deformation velocity can be computed
from deformation velocity components comparative deformation velocity can be computed
from deformation velocity components
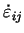 .
In case of axisymmetric piece we getget: .
In case of axisymmetric piece we getget:
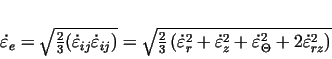 |
(17) |
The values of
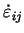 deformation velocity components are as follows: deformation velocity components are as follows:
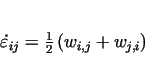 |
(18) |
Taking into account that the piece is in contact with the die in two sides, and,
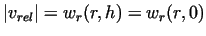 , the friction power can be expressed as follows: , the friction power can be expressed as follows:
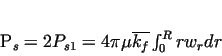 |
(19) |
For the sake of simplicity we perform the calculations for solid cylindrical
pieces at 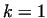 . A similar example solution is available in [8].
Equation (18) takes the following simple scalar form: . A similar example solution is available in [8].
Equation (18) takes the following simple scalar form:
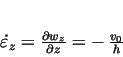 |
(20) |
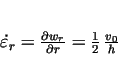 |
(21) |
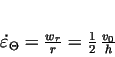 |
(22) |
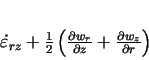 |
(23) |
The value of
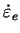 comparative deformaition
velocity can be expressed from (20, 21, 22,
23) as: comparative deformaition
velocity can be expressed from (20, 21, 22,
23) as:
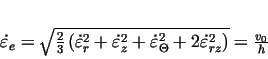 |
(24) |
From equations (5, 6, 7), we obtain:
 , so the introduced velocity field
satisfies the condition of incompressibility.
The comparative deformation velocity come the components of power, can be expressed in the following form: , so the introduced velocity field
satisfies the condition of incompressibility.
The comparative deformation velocity come the components of power, can be expressed in the following form:
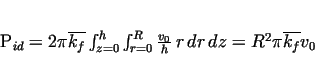 |
(25) |
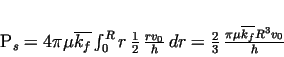 |
(26) |
The total power 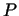 can be determined from the velocity can be determined from the velocity  and the mean force and the mean force  ,
acting on contact surface. ,
acting on contact surface.
 |
(27) |
So the power requirement of forming is:
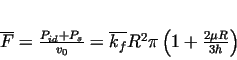 |
(28) |
Equation (28) can be derived also by the average stress method, and is
known as Siebel-formula (see [2,3]).
If 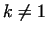 , the velocity field changes according to the actual value of , the velocity field changes according to the actual value of
 . Best value of . Best value of 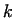 bz the upper bound method minimiyes the following function. bz the upper bound method minimiyes the following function.
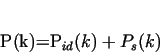 |
(29) |
In the case of 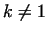 the exprressions for the power are more complicated, because initial conditions
(11, 12) are also more complicated, and the exprressions for the power are more complicated, because initial conditions
(11, 12) are also more complicated, and
Calculations
were performed by using mathematical software MapleV (see [9]), see also [1] for a similar
industrial applications.
| Submitted to HEJ
Manuscript no.: MET-990617-A |  

 |
|