Submitted to HEJ
Manuscript no.: MET-990617-A |  

 |
|
If  , for calculation of ideal and friction power, bilge character also
should be taken into account. For the boundary of integration (relation
(16)) and for definition of the radius , for calculation of ideal and friction power, bilge character also
should be taken into account. For the boundary of integration (relation
(16)) and for definition of the radius 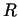 of friction surface
(relation (26)), the function of friction surface
(relation (26)), the function 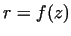 , describing the instantaneous
bilge form, is necessary. It makes the exact definition of the function
more difficult because that it depends on time also, that is , describing the instantaneous
bilge form, is necessary. It makes the exact definition of the function
more difficult because that it depends on time also, that is 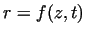 . Considering the
displacement of a point of the function under an elementary . Considering the
displacement of a point of the function under an elementary 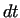 period, the
following equations hold: period, the
following equations hold:
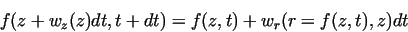 |
(30) |
Expanding the left-hand in terms of Taylr series, we obtain a differential equation
which describes the
the change of the curve in time:
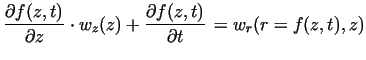 |
|
|
(31) |
If the curvature of the surface is small enough, the first term of the left-hand side
is negligible. Assuming that the initial condition
is cylindrical (i.e.
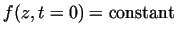 ), and taking into account that ), and taking into account that
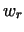 is a quadratic function of is a quadratic function of 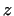 , the solution of differential equation
(31) is also quadratic in , the solution of differential equation
(31) is also quadratic in 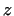 . Therefore
we approximated the profile curve by a second degree regression curve.
Approximation with a second degree curve is quite usual (see e.g. [6])).
Table 1. shows the errors of the approximation
relative to the average radius at different values of the coefficient of
friction ( . Therefore
we approximated the profile curve by a second degree regression curve.
Approximation with a second degree curve is quite usual (see e.g. [6])).
Table 1. shows the errors of the approximation
relative to the average radius at different values of the coefficient of
friction (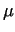 ) and the upset height ( ) and the upset height (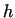 ) see [13]. The initial sizes of the
work piece are: ) see [13]. The initial sizes of the
work piece are:
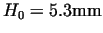 , ,
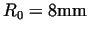 . .
Table 1:
Relative error of approximation
The height of the
upset work piece |
Relative error |
 |
 |
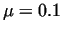 |
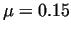 |
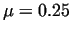 |
| 2.5 |
-- |
6.70768E-05 |
1.73792E-04 |
5.35802E-04 |
| 3 |
1.29048E-05 |
5.45206E-05 |
1.24832E-04 |
3.51149E-04 |
| 3.5 |
1.17484E-05 |
3.84116E-05 |
8.03957E-05 |
2.10181E-04 |
| 4 |
8.11444E-06 |
2.23918E-05 |
4.37545E-05 |
1.07693E-04 |
| 4.5 |
3.80848E-06 |
9.30945E-06 |
1.72268E-05 |
4.03032E-05 |
| 5 |
6.40259E-07 |
1.43069E-06 |
2.53462E-06 |
5.68641E-06 |
|
Table 1. clearly shows that:
- the relative error increases with the coefficient
of friction and with the degree of upsetting;
- for practical purposes, the profile of the work piece can
be approximated with a function of second degree with good accuracy.
Lnowing the profile, one can determine the current volume of the work piece and
the force requirement of the upsetting. The control calculations justified the
volume-consistence with the accuracy of 1-2%.
| Submitted to HEJ
Manuscript no.: MET-990617-A |  

 |
|