Submitted to HEJ
Manuscript no.: MET-990617-A |  

 |
|
For the sake of simplicity in the modeling of the deformation process we
assumed that the coefficient of friction remains constant during the
upsetting. Under such a condition the value of 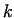 depends only on the current
height of the work piece. If the value of depends only on the current
height of the work piece. If the value of 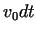 is small enough, the
value of is small enough, the
value of 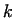 can be considered to be constant during upsetting.
For investigation of the forming process, before upsetting at the cross
section of the piece we adopted a set of ponts, and,
by using relations (11, 12), we determined the new position
of the adopted point for displacement can be considered to be constant during upsetting.
For investigation of the forming process, before upsetting at the cross
section of the piece we adopted a set of ponts, and,
by using relations (11, 12), we determined the new position
of the adopted point for displacement 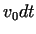 . Then we considered the
new geometry, and so the value of . Then we considered the
new geometry, and so the value of 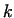 was determined. The procedure can
be repeated while we remain in the validity range of the relation
(11, 32).
At the calculations the value of was determined. The procedure can
be repeated while we remain in the validity range of the relation
(11, 32).
At the calculations the value of 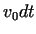 was was 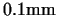 . .
Figure 4:
The variation of the specific power requirement of
forming depending on the value of 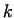 at different degrees of upsetting.
( at different degrees of upsetting.
( , ,
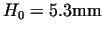 , ,
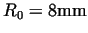 ) )
|
|
The way of calculation can be facilitated by expressing the value of  as
a function of the coefficient of friction as
a function of the coefficient of friction 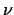 and the height and the height 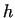 of the piece to be
upset. For a given initial geometry, in a certain range of of the piece to be
upset. For a given initial geometry, in a certain range of 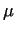 friction
coefficients and height friction
coefficients and height 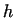 , shown on thw Fig. 6., , shown on thw Fig. 6., 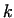 can be approximated with acceptable accuracy
by regression
calculation using a function of the type: can be approximated with acceptable accuracy
by regression
calculation using a function of the type:
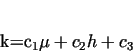 |
(32) |
type of functions.
Figure 5:
The variation of the specific power requirement of forming
depending on the value of 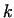 at different values of friction. The upset
height of the work piece is at different values of friction. The upset
height of the work piece is
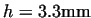 .
( .
(
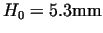 , ,
 ) )
|
|
Figure 6:
Values of 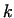 as a function of friction coefficient as a function of friction coefficient  and the
instantaneous
and the
instantaneous 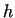 height of the piece
( height of the piece
(
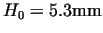 , ,
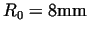 , ,
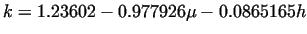 ) )
|
|
Applying the above described method we used an AutoLISP
program. The program upsets the piece for the desired degree (to 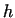 height)
with the given coefficient of friction and in its final stadium draws the
picture of the deformed web of dots and the field of velocity
(Fig. 7 refers). By means of the deformed set of dots the local
deformations can also be studied. height)
with the given coefficient of friction and in its final stadium draws the
picture of the deformed web of dots and the field of velocity
(Fig. 7 refers). By means of the deformed set of dots the local
deformations can also be studied.
Figure 7:
Deformation of the set of points and the instantaneous field of
velocity
|
|
The above modeling makes it possible to investigate the effects of friction
coefficient as well.
Figure:
Effects of friction coefficients
(
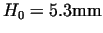 , ,
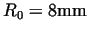 , ,
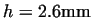 ) )
|
|
Here I present 3 animations with different coefficients of friction:
| Submitted to HEJ
Manuscript no.: MET-990617-A |  

 |
|