|
The calculation of velocity field for ring shaped piesesThe axial component of velocity described by equation (11) can also be applied to ring shaped pieces. The radial component of velocity we can determine from the following initial condition for the differential equation (8) is, where The values Fig. 9 shows some rings with different friction coefficients. Here I present 3 animations with different coefficients of friction: As far as we know, investigation of deformation during upsetting between parallel pressure plates has not been carried out followed the process by animation. |
|

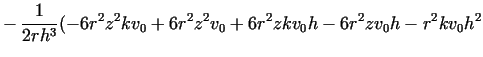
![\includegraphics[width=11cm]{Eps/Fig9.eps}](img227.gif)