HEJ, HU ISSN 1418-7108 Manuscript no.: ANM-980205-A

Download PostScript version Download PDF version

Supplementary files: (unofficial) None.

On a Circulant Representation of the H^(1/2) Seminorm on Rectangles

B. Kiss

Departement of Mathematics, Széchenyi István College
Hédervári u. 3., H-9026 Gyor, Hungary
bkiss@d7.szif.hu


A. Krebsz

Department of Numerical Analysis, Eötvös Lóránd University
Múzeum krt. 6-8., H-1088 Budapest, Hungary
krebsz@cs.elte.hu


G. Molnárka

Departement of Mathematics, Széchenyi István College
Hédervári u. 3., H-9026 Gyor, Hungary
molnarka@d7.szif.hu

Abstract:

The matrix representations of the 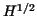$H^{1/2}$ norm are efficient preconditioners for elliptic problems and boundary integral equations of first kind. A new circulant sparse matrix representation has been presented for the 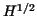$H^{1/2}$ seminorm in the space of bilinear finite elements on a rectangular shaped surface. The matrix contains only 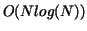$O(Nlog(N))$ non-zero elements where 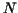$N$ is the number of unknowns.

Keywords: Elliptic problems, domain decomposition, preconditioned conjugate gradient method.

HEJ, HU ISSN 1418-7108 Manuscript no.: ANM-980205-A