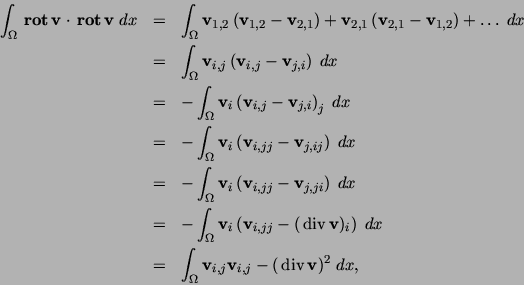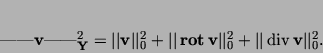|
In the following, we always assume that
|
| (17) |
Let us discuss further spaces, cf. [4]. We define

It is proved in [7] that
We remark that
equipped with the norm
>From [7], we have the following results.
Lemma 2
Assume that 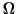 is bounded, Lipschitz-continuous, simply-connected
and
is bounded, Lipschitz-continuous, simply-connected
and 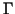 has just one component.
Then there exists a positive constant
has just one component.
Then there exists a positive constant 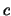 such that
such that
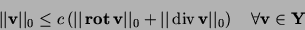
holds.
Proof. See [7], Lemma 3.4.
holds.
Lemma 3
Assume that  is bounded, Lipschitz-continuous, simply-connected
and
is bounded, Lipschitz-continuous, simply-connected
and  has just one component.
Then, the seminorm
has just one component.
Then, the seminorm
is a norm in Y, too.
Proof. Lemma 3 is a direct consequence of Lemma 2.
is a norm in Y, too.
The next lemma requires more than the standard assumptions for technical magnetic field problems. Indeed, electromagnetic devices may have re-entrant corners. Therefore, we will not base our further investigations on Lemma 4.
Lemma 4
Assume further that either 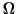 has a
has a
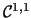 boundary,
or
boundary,
or 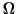 is a convex polyhedron. Then
is a convex polyhedron. Then 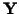 is continuously
imbedded in
is continuously
imbedded in 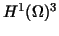 .
.
Proof. See [7], Theorem 3.7.
Manuscript no.: ANM-981030-A | |