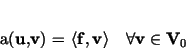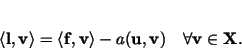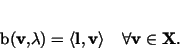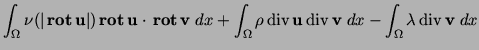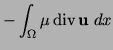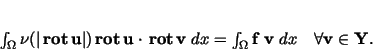HEJ, HU ISSN 1418-7108 Manuscript no.: ANM-981030-A

Nonlinear extension of Brezzi's theorem

The following lemma provides equivalent formulations for the LBB condition in an abstract setting.

Lemma 7   Define the linear operator $B : {\bf X}\longrightarrow {\bf M}^\star$ and its adjoint operator $B^\star : {\bf M}\longrightarrow {\bf X}^\star$ in abstract spaces ${\bf X}$, ${\bf M}$ by

$$\langle B {\bf u}, \mu \rangle = b({\bf u},\mu) \quad \forall \mu\in{\bf M}\quad \forall {\bf u}\in{\bf X}$$ (62)

$$\langle B^\star \lambda, {\bf v} \rangle = b({\bf v},\lambda) \quad \forall {\bf v}\in{\bf X}\quad \forall \lambda \in {\bf M}.$$ (63)

Then, the following formulations of the LBB condition $(1^\circ)$, $(2^\circ)$, $(3^\circ)$ are equivalent.
$(1^\circ)$ $\exists \beta_1 = { \rm const }> 0$ such that

$$\sup_{{\bf v}\in{\bf X}, {\bf v}\neq{\bf0}} \frac{b({\bf ... ...ert\vert\mu\vert\vert _{\bf M}\quad \forall \mu \in {\bf M},$$ (64)

$(2^\circ)$ The operator $B : {{\bf V}_0}^\bot \longrightarrow {\bf M}^\star$ is an isomorphism, and the estimate

$$\vert\vert B{\bf v}\vert\vert _{{\bf M}^\star} \geq \beta_1... ...rt\vert _{\bf X} \quad \forall {\bf v} \in {{\bf V}_0}^\bot$$ (65)

holds, where ${{\bf V}_0}^\bot = \left\{ {\bf u}\in{\bf X}: ({\bf u},{\bf v})_{\bf X}= 0 \quad \forall {\bf v} \in {{\bf V}_0}\equiv \ker B \right\}.$
$(3^\circ)$ The operator $B^\star : {\bf M}\longrightarrow {{\bf V}_0}^0$ is an isomorphism, and the estimate

$$\vert\vert B^\star \mu\vert\vert _{{\bf X}^\star} \geq \bet... ...ert\vert\mu\vert\vert _{\bf M} \quad \forall \mu \in {\bf M}$$ (66)

holds, where ${{\bf V}_0}^0 = (\ker B)^0 \subset {\bf X}^\star$ denotes the polar of ${{\bf V}_0}$, i.e.

$${{\bf V}_0}^0 = \left\{ {\bf l}\in{\bf X}^\star : \langle {\b... ... \quad \forall {\bf v} \in {{\bf V}_0}\equiv \ker B \right\}.$$

Proof. The lemma is proved, e.g., in [3, Lemma 4.2].
Next, we present an extension of Brezzi's theorem to a class of nonlinear problems.

THEOREM 5   Suppose a mixed variational problem in abstract setting
Find $({\bf u},\lambda) \in {\bf X}\times {\bf M}$ such that

  

$${a}({\bf u},{\bf v}) + b({\bf v}, \lambda) = \langle {\bf f},{\bf v} \rangle \quad \forall {\bf v} \in {\bf X},$$ (67)

$$b({\bf u}, \mu) = 0 \quad \forall \mu \in {\bf M},$$ (68)

where the bivariate form $a(.,.)$ is assumed to be linear with respect to its second argument only, and $b(.,.)$ is a bilinear form. Assume that the following conditions are satisfied
(A1) ${\bf f} \in {\bf X}^{\star}$,
(A2) $\exists \beta_2 = { \rm const }> 0$ with

$$\begin{eqnarray*} \vert b({\bf v},\mu)\vert &\leq& \beta_2 \vert\vert{\bf v}\ve... ...f M} \quad \forall {\bf v} \in {\bf X}, \forall \mu\in{\bf M}, \end{eqnarray*}$$

(A3) the LBB (Ladyzenskaya-Babuška-Brezzi) condition, i.e.
$\exists \beta_1 = { \rm const }> 0$ such that

$$\sup_{{\bf v}\in{\bf X}, {\bf v}\neq{\bf0}} \frac{b({\bf ... ...ert\vert\mu\vert\vert _{\bf M}\quad \forall \mu \in {\bf M},$$ (69)

(A4) the strong ${{\bf V}_0}$ - monotonicity of $a$, i.e. $\exists \alpha_1 = { \rm const }> 0$ with

$$a({\bf u},{\bf u} - {\bf v}) - a({\bf v},{\bf u} - {\bf v})... ...ert^2_{\bf X} \quad \forall {\bf u}, {\bf v} \in {{\bf V}_0}$$ (70)

where

$${{\bf V}_0}= {\bf V}(0) = \left\{ {\bf v} \in {\bf X}: b({\bf v},\mu) = 0 \quad \forall \mu \in {\bf M}\right\},$$ (71)

(A5) and the Lipschitz continuity of $a$, i.e., $\exists \alpha_2 = { \rm const }> 0$ with

$$\left\vert a({\bf u},{\bf w}) - a({\bf v},{\bf w}) \right\v... ...{\bf w}\in {\bf X}\quad \forall {\bf u}, {\bf v} \in {\bf X}.$$

Then there exists a unique solution $({\bf u},\lambda) \in {\bf X}\times {\bf M}$.

Proof. >From (A4) and (A5) it follows that the nonlinear problem
Find ${\bf u}\in{{\bf V}_0}$ with

$$a({\bf u},{\bf v}) = \langle {\bf f},{\bf v} \rangle \quad\forall {\bf v}\in{{\bf V}_0}$$ (72)

has a unique solution ${\bf u}\in{{\bf V}_0}$ (see, e.g., [19, Theorem 24.2.]). Then we define ${\bf l}\in {\bf X}^\star$ by

$$\langle {\bf l},{\bf v} \rangle = \langle {\bf f}, {\bf v} \rangle - a({\bf u},{\bf v}) \quad\forall {\bf v}\in{\bf X}.$$ (73)

Since

$$\langle {\bf l},{\bf v} \rangle = 0 \quad\forall {\bf v}\in{{\bf V}_0},$$

we get ${\bf l}\in{{\bf V}_0}^0$, and with Lemma 7 ($3^\circ$) it follows that there exists a unique $\lambda\in{\bf M}$ with

$$b({\bf v},\lambda) = \langle {\bf l},{\bf v} \rangle \quad\forall {\bf v}\in{\bf X}.$$ (74)

Finally, we conclude from ${\bf u}\in{{\bf V}_0}$, (73), (74), that the pair $({\bf u},\lambda) \in {\bf X}\times {\bf M}$ fulfills (67), (68).
Now, we apply Theorem 5 to the variational formulation (VF2).

THEOREM 6   Suppose that ${\bf f}\in{\bf Y}^\star$ and that the material function fulfills (50) and (M1), (M2), (M4) and (M5). Then (55), (56) have a unique solution.

Proof. The assumptions (A1), (A2) and (A3) are verified in the proof of Theorem 2. Further, (A4) and (A5) follow from the Lemmata 5 and 6.
The results of Section 3.4 can be carried over to the nonlinear case without modification.

THEOREM 7   Assume that $\Omega$ is bounded, Lipschitz-continuous and simply-connected. Assume further that ${\bf f} \in H(\div ;\Omega)$ is divergence-free, i.e.,

$$\div {\bf f} = 0.$$ (75)

Then, the unique solution $({\bf u},\lambda)$ of

$$\int_{\Omega} \nu(\vert{ \bf rot }{\bf u}\vert) { \bf rot }{\... ...} \rho \div {\bf u} \div {\bf v} \;dx - \int_{\Omega} \lambda \div {\bf v} \;dx = \int_{\Omega} {\bf f} \; {\bf v} \;dx \quad \forall {\bf v}\in{\bf Y}$$

$$- \int_{\Omega} \mu \div {\bf u} \; dx = 0 \quad \forall \mu\in{\bf M}$$

fulfills

$$\int_{\Omega} \nu(\vert{ \bf rot }{\bf u}\vert) { \bf ... ...ega} {\bf f} \; {\bf v} \;dx \quad \forall {\bf v}\in{\bf Y}.$$ (76)

Proof. Coincides with that of Theorem 4. Indeed, the only term in (35) involving $\nu$ is not changed during the proof of Theorem 4.
Thus, the variational formulation of the nonlinear problem is adequate to the physical problem. Again, we have $\lambda=0$ such that we can omit the $\lambda$-term and solve the coercive problem:
(VF2$^\star$) Find ${\bf u} \in {\bf Y}$ such that

$$\int_{\Omega} \nu(\vert{ \bf rot }{\bf u}\vert) { \bf ... ...ega} {\bf f} \; {\bf v} \;dx \quad \forall {\bf v}\in{\bf Y}.$$ (77)

The unique solution ${\bf u}$ of (VF2$^\star$) coincides with the ${\bf u}$ in the solution of (VF2).

HEJ, HU ISSN 1418-7108 Manuscript no.: ANM-981030-A