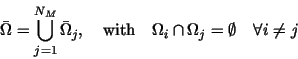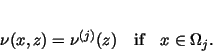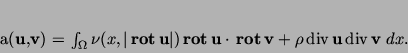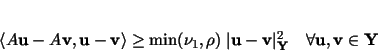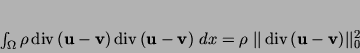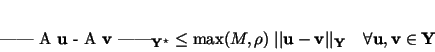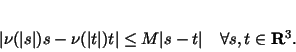HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-981030-A
| 

 |
|
In many practical cases, the nonlinear behaviour of ferromagnetic
materials cannot be neglected.
Therefore, we extend the analysis of 2D monotone, Lipschitz continuous
nonlinear problems (see [8]) to three dimensions.
Let  be decomposed into subdomains be decomposed into subdomains
representing materials with different magnetic properties.
We assume that the function
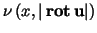 in (8)
depends on the position
in (8)
depends on the position
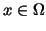 ,
but ,
but 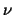 is always the same function in one of the is always the same function in one of the 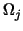 , i.e., , i.e.,
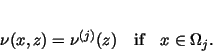 |
(50) |
We suppose the following properties of
the functions
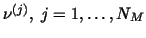 which are justified by the physical model (cf. [8]):
which are justified by the physical model (cf. [8]):
- (M0)
-
![$ \nu^{(j)}(z) = \nu^{(j)}_1 = \mbox{ const. }
\quad \forall z \in [0,z^{(j)}_1], $](img285.gif)
- (M1)
-
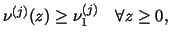
- (M2)
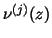 is a monotonic increasing function, is a monotonic increasing function,
- (M3)
-
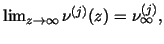 where
where
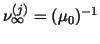 for ferromagnetic
materials, for ferromagnetic
materials,
- (M4)
- there exists
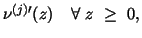 and there exists a constant and there exists a constant
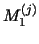 with with
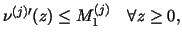
- (M5)
- there exists a constant
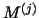 with with
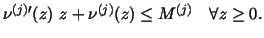
Let 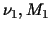 and and 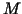 be the global constants with be the global constants with
We define the bivariate form
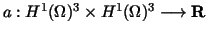 which is nonlinear in its first argument, but linear in its second, by
which is nonlinear in its first argument, but linear in its second, by
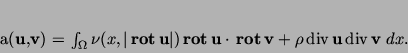 |
(54) |
Then, the variational formulation for the problem
(8), (9) can be written as:
(VF2) Find a pair
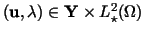 such that
such that
where the bilinear form 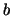 is the identical as in (22).
Now, we prove monotonicity and Lipschitz
continuity of the form is the identical as in (22).
Now, we prove monotonicity and Lipschitz
continuity of the form 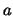 resp. the (nonlinear) operator resp. the (nonlinear) operator
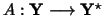 defined by
defined by
Lemma 5
Assume (M1) and (M2). Then  is strongly monotone,
i.e., the inequality
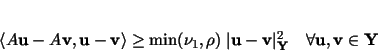 |
(57) |
holds.
Proof.
The proof is similar to the proof of Lemma 2.1 in [8].
We consider vectors
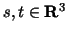 , and assume that , and assume that
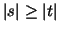 holds without loss of generality.
Then, we get holds without loss of generality.
Then, we get
and from (M1) and (M2) it follows that
holds.
Setting
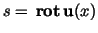 and and
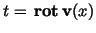 and integrating we obtain and integrating we obtain
and with
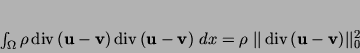 |
(58) |
and Lemma 3 we get the
estimate (57).
Lemma 6
Suppose that (M4) and (M5) hold.
Then  is Lipschitz-continuous, i.e., the
inequality
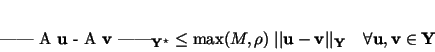 |
(59) |
holds.
Proof.
>From (M4) and (M5) we obtain
and by the mean value theorem we get
 |
(60) |
Consider vectors
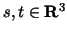 .
The same calculation as in the proof of Lemma 2.2 in [8]
yields .
The same calculation as in the proof of Lemma 2.2 in [8]
yields
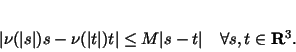 |
(61) |
We set
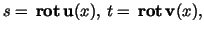 multiply with multiply with
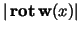 ,
and take the integral over ,
and take the integral over 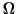 . The result is . The result is
and with well-known estimates, an equation for the 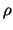 term,
and Lemma 3 we obtain term,
and Lemma 3 we obtain
and the desired estimate (59).
| HEJ, HU ISSN 1418-7108
Manuscript no.: ANM-981030-A
| 

 |
|