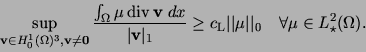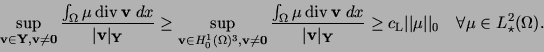HEJ, HU ISSN 1418-7108 Manuscript no.: ANM-981030-A

The Brezzi theorem

We recall the Brezzi theorem, e.g. from [3].

THEOREM 1   Suppose a mixed variational problem in abstract setting
Find $({\bf u},\lambda) \in {\bf X}\times {\bf M}$ such that

  

$${a}({\bf u},{\bf v}) + b({\bf v}, \lambda) = \langle {\bf f},{\bf v} \rangle \quad \forall {\bf v} \in {\bf X},$$ (25)

$$b({\bf u}, \mu) = \langle g, \mu \rangle \quad \forall \mu \in {\bf M}.$$ (26)

Assume that the following conditions are satisfied
(A1) ${\bf f} \in {\bf X}^{\star}$, $g \in {\bf M}^{\star}$,
(A2) $\exists \alpha_2 = { \rm const }> 0$ and $\beta_2 = { \rm const }> 0$ with

$$\begin{eqnarray*} \vert a({\bf u},{\bf v})\vert &\leq& \alpha_2 \vert\vert{\bf ... ...f M} \quad \forall {\bf v} \in {\bf X}, \forall \mu\in{\bf M}, \end{eqnarray*}$$

(A3) the LBB (Ladyzenskaya-Babuška-Brezzi) condition, i.e.
$\exists \beta_1 = { \rm const }> 0$ such that

$$\sup_{{\bf v}\in{\bf X}, {\bf v}\neq{\bf0}} \frac{b({\bf ... ...ert\vert\mu\vert\vert _{\bf M}\quad \forall \mu \in {\bf M},$$ (27)

(A4) the ${{\bf V}_0}$ - ellipticity, i.e. $\exists \alpha_1 = { \rm const }> 0$ with

$$a({\bf v},{\bf v}) \geq \alpha_1 \vert\vert{\bf v}\vert\vert^2_{\bf X} \quad \forall {\bf v} \in {{\bf V}_0}$$ (28)

where

$${{\bf V}_0}= {\bf V}(0) = \left\{ {\bf v} \in {\bf X}: b({\bf v},\mu) = 0 \quad \forall \mu \in {\bf M}\right\}.$$ (29)

Then there exists a unique solution $({\bf u},\lambda) \in {\bf X}\times {\bf M}$ and the a-priori estimates

$$\begin{eqnarray*} \vert\vert{\bf u}\vert\vert _{\bf X}&\leq& \frac{1}{\alpha_1}... ...{\alpha_1} \right) \vert\vert g\vert\vert _{{\bf M}^{\star}} \end{eqnarray*}$$

hold.

Proof. See, e.g., [4].
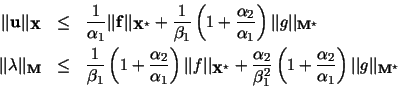
We apply Theorem 1 to the variational formulation (VF1).

THEOREM 2   Suppose that ${\bf f}\in{\bf Y}^{\star}$, $\rho = { \rm const }> 0$ and that $\nu(x)$ is a piecewise constant function fulfilling

$$0 < \underline{\nu} \leq \nu(x) \leq \bar{\nu}.$$ (30)

Then (23), (24) has a unique solution $({\bf u},\lambda) \in {\bf Y}\times L^2_\star(\Omega)$ for which a-priori estimates

$$\begin{eqnarray*} \vert{\bf u}\vert _1 &\leq& \frac{1}{c_{\rm L}} \vert\vert{... ...t)}{c_{\rm L}}) \vert\vert{\bf f}\vert\vert _{{\bf Y}^{\star}} \end{eqnarray*}$$

hold.

Proof. We have to verify the assumptions of Theorem 1.
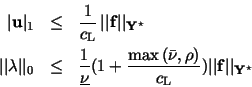
(A1) It is the assumption, and $g=0$.
(A2) Applying Lemma 3 we get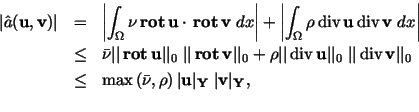

$$\begin{eqnarray*} \left\vert \hat{a}({\bf u},{\bf v}) \right\vert &=& \left\v... ...t) \vert{\bf u}\vert _{\bf Y}\; \vert{\bf v}\vert _{\bf Y}, \\ \end{eqnarray*}$$

i.e., we can set 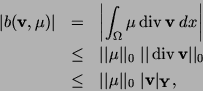$\alpha_2 = \max \left( \bar{\nu}, \rho \right)$, and

$$\begin{eqnarray*} \left\vert b({\bf v},\mu) \right\vert &=& \left\vert \int_{... ...\leq& \vert\vert\mu\vert\vert _0 \; \vert{\bf v}\vert _{\bf Y}, \end{eqnarray*}$$

i.e. $\beta_2 = 1$.
(A3) The LBB condition has been proved for the Stokes problem, cf. e.g. [6, Theorem 3.7]. There exists a constant $c_{\rm L} > 0$ with

$$\sup_{{\bf v}\in H_0^1(\Omega)^3, {\bf v}\neq{\bf0}} \fra... ...ert\mu\vert\vert _0 \quad \forall \mu \in L^2_\star(\Omega).$$ (31)

>From Lemma 1 and (20) we get $\vert{\bf v}\vert _{\bf Y}= \vert{\bf v}\vert _1 \;\forall {\bf v}\in H_0^1(\Omega)^3$, and with $H_0^1(\Omega)^3 \subset {\bf Y}$ it follows that

$$\sup_{{\bf v}\in {\bf Y}, {\bf v}\neq{\bf0}} \frac{ \int_... ...ert\mu\vert\vert _0 \quad \forall \mu \in L^2_\star(\Omega).$$ (32)

(A4) We can prove ellipticity for the whole space ${\bf Y}$, i.e.

 

$$\hat{a}({\bf v},{\bf v}) \geq \underline{\nu} \vert\vert{ \bf rot }{\bf v}\vert\vert _0^2 + \rho \vert\vert\div {\bf v}\vert\vert _0^2 \quad \forall {\bf v} \in {\bf Y}$$

$$\hat{a}({\bf v},{\bf v}) \geq \min \left( \underline{\nu}, \rho \right) \vert{\bf v}\vert _{\bf Y}^2 \quad \forall {\bf v} \in {\bf Y},$$ (33)

and $\alpha_1 = \min \left( \underline{\nu}, \rho \right)$.
We remark that it may be useful to choose $\rho$ depending on the actual coefficients $\nu$, e.g., $\underline\nu\leq \rho \leq\bar\nu$.

HEJ, HU ISSN 1418-7108 Manuscript no.: ANM-981030-A